2016年駒場東邦の問題です。
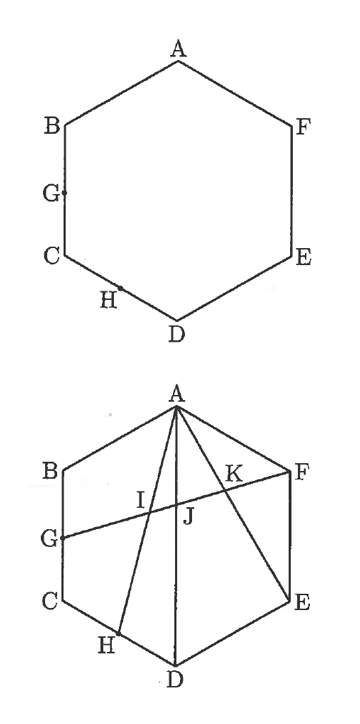
図のような正六角形ABCDEFがあります。辺BC,CDの真ん中の点をそれぞれGHとします。
(1)三角形AGEの面積は正六角形ABCDEFの面積の何倍ですか。
(2)FGとAHが交わる点をI、FGとADが交わる点をJ、FGとAEが交わる点をKとします。
次の長さの比を最も簡単な整数の比で求めなさい。
① BGとAJ
② AKとKE
(3)正六角形ABCDEFの面積を12cm2とするとき、三角形AIKの面積を求めなさい。
【解説と解答】
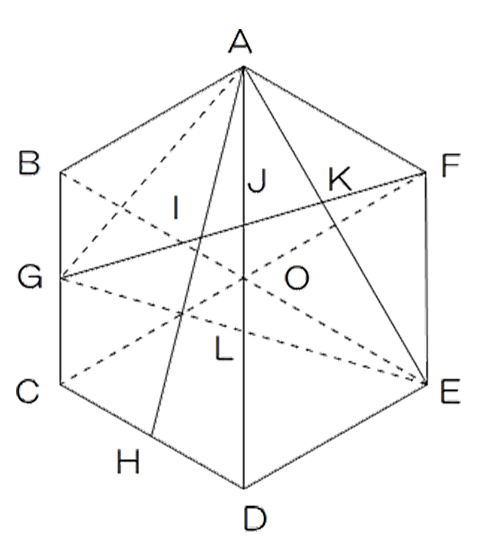
(1)全体の面積を【6】とすると、三角形AFEは【1】、三角形ABGは【0.5】、三角形CDEも【1】、三角形GCEも【1】だから、三角形AGEは【6】-【3.5】=【2.5】
したがって$$\frac{25}{60}$$=$$\frac{5}{12}$$
(答え)$$\frac{5}{12}$$倍
(2)FEの長さを(1)とすると、JLは(0.5) AD=(2)からAJ=(1.5)÷2=(0.75) BG=(0.5)よりBG:AJ=2:3
AK:KE=AJ:FE=0.75:1=3:4
(答え)BG:AJ 2:3 AK:KE 3:4
(3)
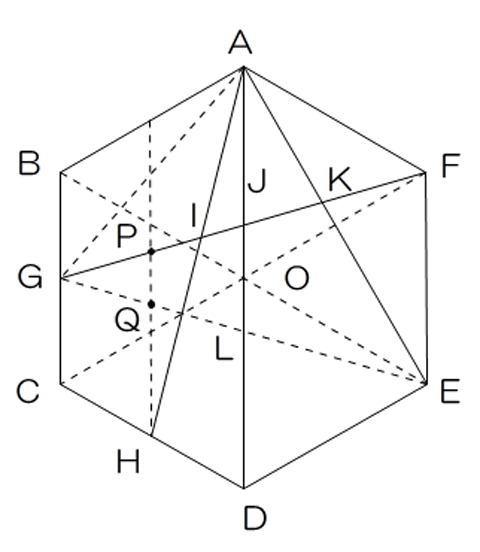
HからADに平行に線を引き、GEとの交点をQ、GFとの交点をPとするとPQ=(0.25) HQ=(1.5-0.25)÷2=0.625 HP=0.875 AJ=0.75だからAI:IH=0.75:0.875=6:7
したがって正六角形の6分の1の正三角形が2cm2になるので、三角形AJIは底辺が4分の3、高さが半分×13分の6だから13分の3。
三角形AJKは底辺が4分の3で高さが7分の3だから、結局三角形AIKは底辺が4分の3、高さが13分の3+7分の3で、91分の60
したがって2×$$\frac{3}{4}$$×$$\frac{60}{91}$$=$$\frac{90}{91}$$
(答え)$$\frac{90}{91}$$cm2
受験で子どもと普通に幸せになる方法、本日の記事は
自分の机で勉強する
5年生の教室から
付属校、系属校、推薦枠
中学受験 算数オンライン塾
12月20日の問題
じっくり算数教室
第1回 「植木算」
3・4年生を対象に、塾の授業形式で植木算を学習します。先生の話を聞きながら、ノートをとる練習も課題としています。
じっくり算数教室の教材