2015年早稲田中学の問題です。
図1のような、地面に垂直に立っている半径12cmの円板があり、Oを中心として自由に回転できるようになっている。円板にはピンと糸を使っておもりをつるすことができる。ただし、ピンと糸の重さは考えないものとする。また、いずれの問いでも初めのA、0、Bの高さは同じであったとする。以下の問いに答えよ。
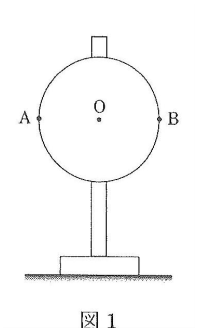
問1 図2のように重さの等しい2つのおもりを円板のAとCにつるした。円板はどちら向きに何度回転して静止するか。向きは図中のあ、いのどちらかで答えよ。
問2 図3のように円板のAに10gのおもりを、Dに重さのわからないおもりをつるしたところ、円板は回転せず静止した。Dにつるしたおもりは何gか。
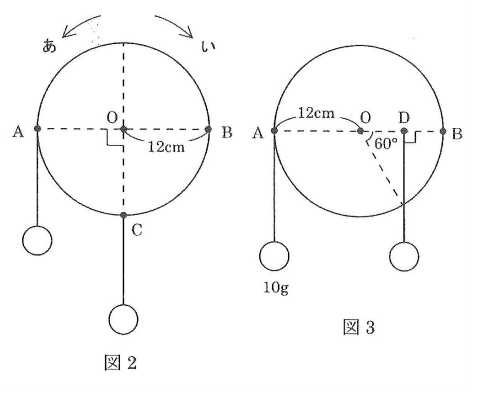
問3 図4のように円板のEに20g、Fに10gのおもりをつるしたところ、円板は少し回転して静止した。円板はどちら向きに何度回転して静止するか。向きは図中のあ、いのどちらかで答えよ。
問4 図5のように円板のA、Bに1Ogのおもりをつるしたところ、円板は回転せず静止した。次に10gのおもりを円板の円周上のア~コの1か所につるしたところ、Aはケの位置へ、Bはエの位置へ移動し、円板は静止した。このときつるした位置をア~コから選び、記号で答えよ。ただし、円内の線は円を12等分している。
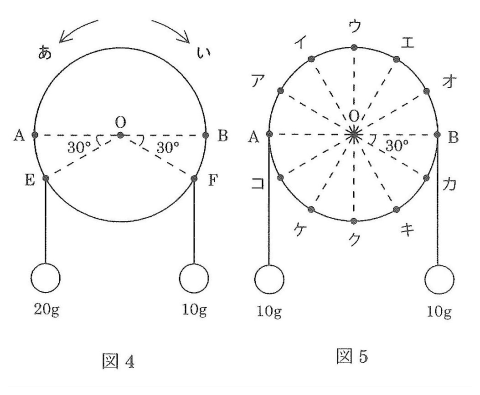
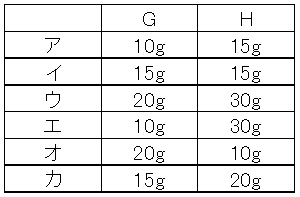
問5 図6のように円板のG、H、Iにおもりをつるしたところ、円板は回転せず静止した。Iにつるすおもりの重さを40gとすると、G、Hにつるすおもりの重さはそれぞれ何gか。ア~カの中からあてはまるものをすべて選び、記号で答えよ。ただし、図中のOGは12cm、0Hは4cm、0I6はcmである。また、円内の線は円を6等分している。
【解説と解答】
問1 A側が下がってOAとOCが図2のOCを対象の軸として静止します。したがってあの方向に45°回転します。
(答え)あ 45°
問2
ODは12cmの半分の6cmになっているので、Dのおもりの重さは10×2=20gです。
(答え)20g
問3
全体が30°、あの方向に回転すれば、下図のようにOG=6cmとなって20:10でつりあいます。
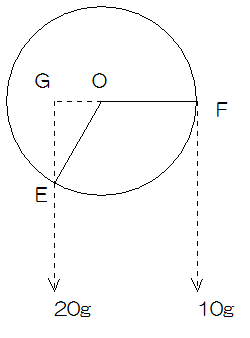
したがってあの方向に30°回転します。
(答え)あ 30°
問4
60°回転したところで新しくつるしたおもりはケの位置に来るので、コにつるしたことになります。
(答え)コ
問⑤
Iは支点Oからまっすぐ右に3cmのところにあり、HはOからまっすぐ左に2cmのところにあります。したがって
G×6+H×2=40×3=120
この式にあてはまるのイとエです。
(答え)イ、エ
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
筆箱はしまうもの?
=============================================================
中学受験 算数オンライン塾
1月9日の問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村


