2011年早稲田中学の問題です。
長さ100cmで太さが一様でない棒AB、重さ100gの輪じく(じくの半径が5cm、輪の半径が20cm)、重さがそれぞれ20g、40g、60g、80g、100gのおもり1個ずつを用意し、いろいろなことを調べた。以下の問いに答えよ。
この棒ABを水平なゆかの上に置き、図1のように棒のはしAにばねはかりをつけて、Aをわずかに持ち上げて重さをはかったら30gであった。また、もう一方のはしBについて同じようにはかると、70gであった。
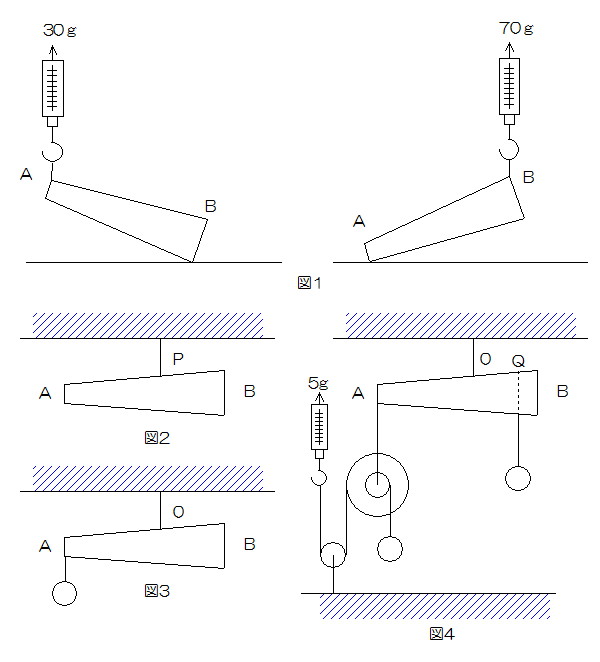
問1 棒ABの重さは何gか。
問2 図2のように、棒ABをP点でつるしたら棒は水平になった。P点は棒ABのはしAから何cmのところか。
問3 図3のように、棒ABのはしAにおもりをつるし、棒ABを真ん中のO点でつるしたら棒は水平になった。Aにつるしたおもりの重さは何gか。
問4 図4のように、輪じくを棒ABのA点でつるした。じくにおもりをつるし、輪に巻いた糸を地面に固定したかっ車に通して手でばねはかりを支えたところ、ばねはかりは5gを示した。また、棒ABをO点でつるし、棒ABのQ点におもりをつるしたところ棒は水平になった。
(1)じくにつるしたおもりの重さは何gか。
(2)Q点につるしたおもりの重さは何gか。
(3)Q点は棒ABのはしBから何cmのところか。
問1 Aをつるしたとき30g Bをつるしたとき70gですからこの棒の重さはその和になります。
30+70=100g
(答え)100g
問2
A:B=3:7ですからPはAから全体の(3+7)分の7のところに重心がきます。
ABの長さは100cmですから
100×7/10=70㎝
(答え)70㎝
問3
Oから右に20㎝のところに重心100gがかかります。それをOから左に50㎝のところでつりあわせるので、
100×20÷50=40gがおもりの重さになります。
(答え)40g
問4
(1)輪の半径が20㎝ じくの半径が5㎝ですからじくにつるしたおもりは
5g×20÷5=20gになります。
(答え)20g
(2)したがってAには輪じくの重さ100gとおもり20gと5gの合計125gがかかっています。
Oを支点にしたとき、反時計周りの回転力は
125×50=6250
ぼうの重さの回転力は時計回りに20×100=2000なので
6250ー2000=4250 不足します。
おもりは20g、40g、60g、80g、100gですがOからBまで50㎝しかないので、100gしかこの不足する回転力を補えるおもりはありません。
4250÷100=42.5cm がQのOからの距離になるので、50-42.5=7.5
(2)(答え)100g
(3)(答え)7.5cm
になります。おもりの重さと距離がともにわかりませんが、おもりの重さが限られているので、解ける、という問題です。
問題を良く読んで条件を見落とさないようにしてください。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
ミスが増える原因
==============================================================
中学受験 算数オンライン塾
8月11日の問題
==============================================================









