2012年世田谷学園の問題です。
重さが400g、長さが100cmで太さが一様な棒ABがあります。この棒ABと輪軸とおもりを使って図のような装置をつくりました。
棒ABが水平になるように板でおもりイを支えています。おもりウの重さは350gです。次の問いに答えなさい。

(1)糸1にかかる重さは何gですか。
(2)おもりイが板をおす力を150gとすると糸2にかかる力は何gですか。
(3)おもりイは何gですか。

(1)
棒ABは均質な棒ですから、重心が中心にくるので400÷2=200gがAにつながる糸とBにつながる糸にそれぞれかかります。
輪軸の長い方の半径が7.5cmですから、200×7.5÷5=300gが糸1にかかる重さになります。
(答え)300g
(2)おもりイは350gですが、板を下から150gの力で支えるので、糸2には350-150=200gかかります。
(答え)200g
(3)糸1にかかる重さが300gで糸2にかかる重さが200gですから、その差がおもりアの重さになります。
したがって300-200=100
(答え)100g
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
自由と奔放
==============================================================
中学受験 算数オンライン塾
5月4日の問題
==============================================================

==============================================================
お知らせ
算数5年前期第15回 算数オンライン塾「まとめのテスト」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村


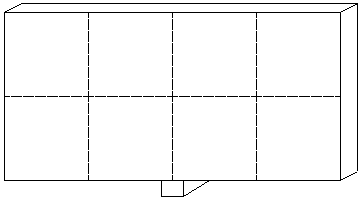
 図6
図6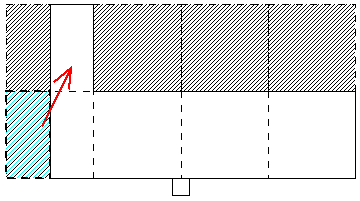 図7
図7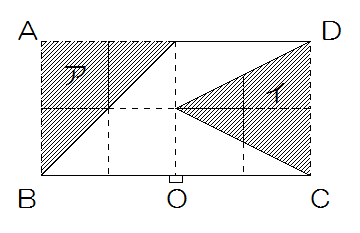 図8
図8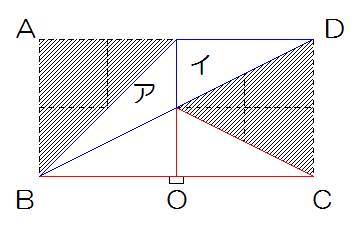
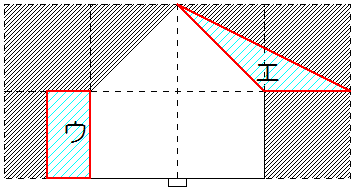 図9
図9 図10
図10
 図1
図1 図2
図2 図3
図3 図4
図4