2017年明大明治の問題です。
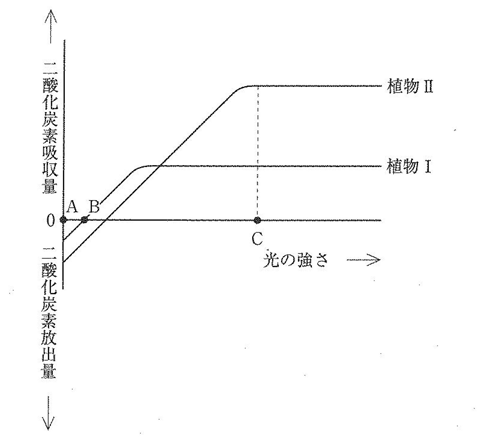
次のグラフは、2種類の植物Ⅰ・Ⅱに当てる光の強さを変えていったときの、光の強さと二酸化炭素の吸収量・放出量の関係を表したものです。なお、グラフのたて軸は、同じ面積の葉が一定時間に吸収・放出した二酸化炭素量を示しています。グラフを見て、問いに答えなさい。
(1)植物IにA.Bの強さの光を当てたときの説明として正しいものを選び、それぞれア~カの記号で答えなさい。
ア 光合成も呼吸も行っていない。
イ 光合成のみを行っている。
ウ 呼吸のみを行っている。
エ 光合成も呼吸も行っているが、光合成量の方が多い。
オ 光合成も呼吸も行っているが、呼吸量の方が多い。
カ 光合成も呼吸も行っていて、光合成量と呼吸量は同じである。
(2)植物Ⅱは、日当たりのよい場所でよく成長し 日かげでは成長しにくい植物です。このような植物を何とよんでいますか。また、これにあてはまる植物を選び、ア~オの記号で答えなさい。
ア アカマツ イ クヌギ ウ シイ エ ススキ オ クスノキ
(3)植物I・ⅡにCの強さの光を当てると、どちらの植物も二酸化炭素を吸収します。二酸化炭素と水、光によって、植物のなかでつくられる物質は何ですか。
【解説と解答】
(1)Aは光が当たっていないので、呼吸のみを行っています。Bはみかけは二酸化炭素の発生量が0ですが、呼吸による発生量と光合成による消費量が等しくなっています。
(答え)Aウ Bカ
(2)日当たりの良いところで成長する植物を陽生植物といいます。これにあたるのはアカマツ、クヌギ、ススキです。
(答え)(名称)陽生植物(記号)ア・イ・エ
(3)片方だけを答えないようにしてください。
(答え)酸素・でんぶん
受験で子どもと普通に幸せになる方法、本日の記事は
過去問をやっていくと
5年生の教室から
式を書く習慣
今日の慶應義塾進学情報
長い夏休み