「各校の入試問題から」カテゴリーアーカイブ

立体の切断に関する問題

2017年聖光学院の問題です。

図１は１辺の長さが１ｃｍである立方体を３段積み重ねた図です。これと同じように８段積み重ねたものが図２の立体です。この立体の１段目から８段目までを３点Ｐ，Ｑ，Ｒを通る平面で切ったとき，点Ａを含む方の立体の体積は何ｃｍ３ですか。

【解説と解答】

図のようになっていくので、切れている立方体は１、２、３、･･･となっていくので
（１＋８）×８÷２＝36個
１つが1×1÷2×1÷3＝1/6　全部で1/6×36＝6cm３が切り落とされます。
全体は１＋３＋６＋10＋15＋21＋28＋36＝120cm3になるので
したがって残るのは120-6＝114cm3
(答え）114cm3

受験で子どもと普通に幸せになる方法、本日の記事は
忘れてる！？

5年生の教室から
睡眠優先

今日の慶應義塾進学情報
募集要項配布

にほんブログ村

月に関する問題

2017年東邦大東邦の問題です。

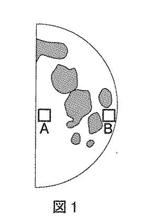
図１は，ある冬の日の午後９時に千葉県習志野市で観察した半月のようすをスケッチしたものです。これについて次の（１）～（４）の問いに答えなさい。

（１）この半月はどの方位の空に見えましたか。もっとも適切なものを，次の１～４から一つ選び,番号で答えなさい。

　　１　北東　　　２　北西　　　３　南東　　４　南西

(２)この半月を望遠鏡で観察したとき，図１のＡの部分とＢの部分にある円形で同じ大きさのクレーターを比べると,それぞれどのように見えますか。もっとも適切なものを，
　　次の１～４から一つ選び，番号で答えなさい。

　　１　どちらも円形に見えるが，Ａの部分にあるクレーターの方が小さく見える
　　２　どちらも円形に見えるが，Ｂの部分にあるクレーターの方が小さく見える
　　３　Ａの部分にあるクレーターは(注）だ円形に　Ｂの部分にあるクレーターは円形に見える
　　４　Ａの部分にあるクレーターは円形に　Ｂの部分にあるクシーターはだ円形に見える

　　(注)　だ円形…円を細長くした形

(３)オーストラリアのシドニーで同じ日の午後９時(現地での時闘)に月を観察しました。
　　この月について，見える方位と，明るい部分の形の組み合わせとしてもっとも適切なものを，あとの１～８から一つ選び，番号で答えなさい。

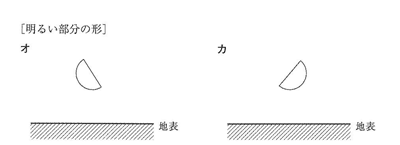
　　[方　位] 　　ア　北東　　　イ　北西　　　ウ　南東　　　エ　南西
１　ア，オ　　　　　２　ア，カ　　　　　３　イ，オ　　　　４　イ，カ
５　ウ，オ　　　　　６　ウ，カ　　　　　ア　エ，オ　　　　８　エ，カ

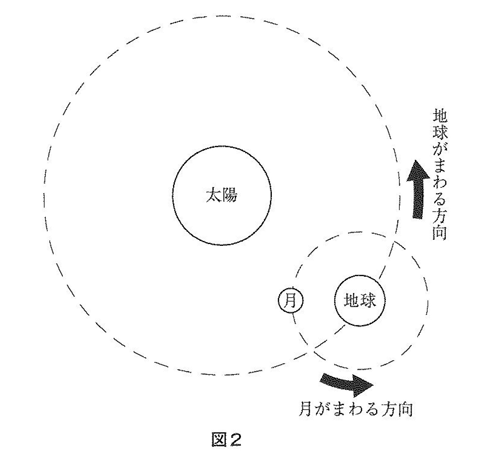
（４）地球は，自ら回転しながら太陽のまわりを回る天体です。月も，自ら回転しながら地球のまわりを回る天体です。地球が太陽のまわりを回る向きと月が迪球のまわりを　回る向きは同じです。図２は，それらを模式的に表したものです。いま，地球が太湯のまわりを360日で一周回り，月の明るい部分の形が30日ごとに同じ形になるとした場合，月が圸球のまわりを一周（360 ° ）回るには何日かかりますか。小数第２位を四捨五入して，小数第１位まで答えなさい。ただし，月の明るい部分の形が30日ごとに同じ形になるのは，地球から見た太陽と月の位置関係が同じになるためです。

【解説と解答】
（１）上弦の月ですから、南中が18時。観察したのが21時ですから南西の方角に見えます。
（答え）４
（２）同じ大きさのクレーターですから、Bの方がだ円形に見えます。
（答え）４
（３）オーストラリアでは、月は北中し、月の満ち欠けは日本と逆に見えます。したがって下弦の月になり、北西の方角に見えます。
（答え）３
（４）満月から次の満月の位置にくるまで30日かかるので、地球は30°公転します。月はしたがって360＋30＝390°公転しなければならないので、390÷30＝13°
したがって360÷13＝27.69･･･となり、27.7日が公転周期です。
（答え）27.7日

受験で子どもと普通に幸せになる方法、本日の記事は
受験生になる

6年生の教室から
学校の宿題

中学受験　算数オンライン塾
7月22日の問題

にほんブログ村

速さに関する問題

2017年東邦大東邦中学の問題です。

Ｐ町とＱ町は1.2km離れています。Ａ君はＰ町を、Ｂ君はＱ町を同時に出発し、この２つの町を歩いて往復します。２人が初めて出会ったのは出発してから６分後でした。２人が初めて出会った後に　Ａ君だけ歩く速さを変えました。Ａ君はＱ町を、Ｂ君はＰ町をそれぞれ折り返した後、２人は初めて出会った地点で再び出会いました。はじめのＡ君の歩く速さとＢ君の歩く速さの比は、５：３でした。このとき、次の問いに答えなさい。

（1）２人が初めて出会うまでのＡ君の歩く速さは分速何ｍか求めなさい。
（2）２人が初めて出会った後のＡ君の歩く速さは分速何ｍか求めなさい。

【解説と解答】
(1)2人が初めて会ったのが6分後ですから、1200m÷6＝200m　200÷（3＋5）×5＝125mが最初のA君の速さです。
（答え）125m

(2)B君の速さは分速75mですから、75×6＝450m
1200－450＝750mが残りの距離になるので、750×2÷75＝20分後にそこに戻ります。
A君は450×2＝900ｍを20分で往復すれば良いので、900÷20＝45
（答え）45m

「映像教材、これでわかる比と速さ」（田中貴）