2016年雙葉学園中学の問題です。
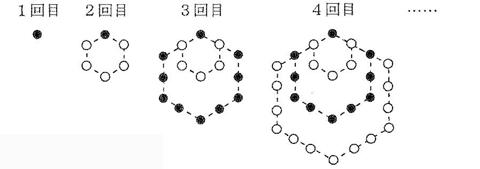
たくさんある黒と白の碁石を図のように並べていきます。
1回目は、黒の碁石を1個置きます。2回目は白、3回目は黒、4回目は白、と、正六角形の形になるように加えていきます。
(1)3回目までに並べた碁石は全部で15個です。32回目までに並べた碁石は全部で何個ですか。
(2)黒の碁石が白の碁石よりも93個多くなるのは、何回目まで並べたときですか。
(3)このように並べた碁石を、1段目に1個、2段目に2個、3段目に3個・・・と、正三角形の形になるように並べかえます。例えば、2回目までに並べた碁石を並べかえると、右の図のようになります。100回目までに並べた碁石を並べかえると、何段の正三角形ができますか。
【解説と解答】
(1)増える個数でみると1回目は1個、2回目は5個、3回目は9個 4回目は13個と4個ずつ増えていきます。
したがって32回は1+4×31=1+124=125個増えるので
全部では(1+125)×32÷2=126×16=2016個
(答え)2016個
(2)奇数番目に増えるのが黒、偶数番目に増えるのが白です。
差は1回目が1 、2回目が4、3回目が5、4回目が8、5回目が9個、というように偶数回は4の倍数、奇数回は4の倍数+1になります。偶数回の場合、回期÷2×4=差の個数です。
93個ですから奇数。なので、(93-1)÷4×2=46回目がその前の偶数回ですから、47回目
(答え)47回目
(3)100回目に増える個数は1+4×99=397
合計の個数は(1+397)×100÷2=19900個
三角形上に並べるとn段まで行けば
(1+n)×n÷2=19900
19900×2=39800をを分解すると199×200になるから、199段目まで並べたことになります。
(答え)199段目
============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
上位校の問題が難しくなる理由
=============================================================
中学受験 算数オンライン塾
5月10日の問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村