2015年栄光学園の問題です。
オセロの駒(片面が白、もう片面が黒の円形の駒)を何枚か円状に並べ、時計回りに2つ飛ばしで裏返していくとき、次の間に答えなさい。
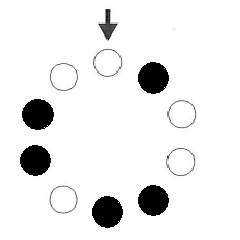
(1)10枚の駒を、すべて表が白になるように並べ(図1)、矢印の指す駒から裏返していきます。例えば、3回裏返すと図2のようになります。
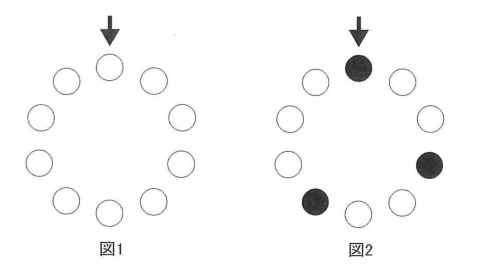
1) 図1の配置から10回裏返すと駒の白黒の配置はどのようになるか、図2にならってかきなさい。
2) 図1の配置から何回裏返すと再び図1の配置にもどるか答えなさい。
3) 図1の配置から2015回裏返すと駒の白黒の配置はどのようになるかかきなさい。
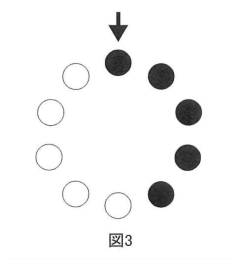
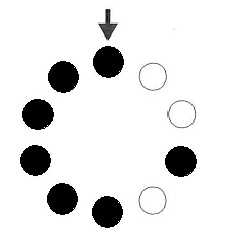
(2)10枚の駒を図3のように並べ、矢印の指す駒から裏返していきます。これを続けていくとき、黒の枚数は最多で何枚になるか答えなさい。また、初めてそうなるときの駒の白黒の配置はどうなるかかきなさい。
(3)何枚かの駒を並べて裏返していったとき、50回で再び元の配置にもどりました。このとき、駒は何枚ありましたか。考えられるものをすべて答えなさい。
【解説と解答】
(1)
1)
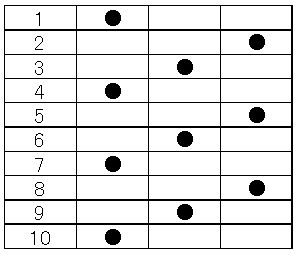 表1
表1
から全部裏返ります。
(答え)
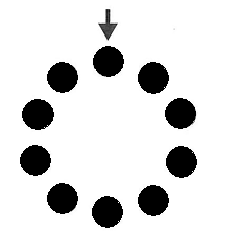
2)11回目は1番が白になるので、そうなるとすべてが白になるのにはあと10回かかるので、合計20回です。
(答え)20回
3)2015÷20=100・・・15回ですから、全部黒になってそのあと5回です。表1から白になるのが1、3、4、7、10なので、以下のようになります。
(答え)
(2)下図のように動きます。
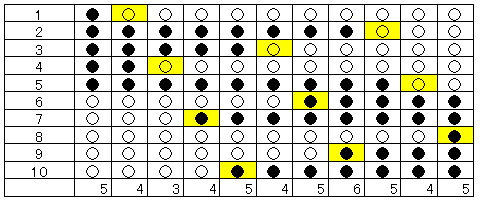 表2
表2
このとき3回目で黑が3になることがるので、逆に13回目で黑が7になることになります。
したがってその図は下のようになります。
(3)
10個の場合は、20回で元に戻りました。
すべての駒が2回あるいは偶数回動いて、もとに戻ります。
50回で戻るためには25×2か5×10しかないので、駒の数は25枚か5枚になります。
次に、駒の枚数が3の倍数であるときを考えます。
この進み方では、駒の枚数が3の倍数であるとき、1周するともとに戻ります。
駒の数が【3】枚あるとき、変わるのは【1】枚だけです。これが2回変わればいいので、【2】=50となる数が3の倍数の時に当てはまります。
したがって50÷2×3=75枚のとき、50回で元の位置に戻ります。
(答え)5枚、25枚、75枚
「映像教材、これでわかる数の問題」(田中貴)
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
遊んじゃいけない、ということはない
==============================================================
中学受験 算数オンライン塾
5月26日の問題
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

