2020年聖光学院の問題です。
植物について,次の(1)~(7)の問いに答えなさい。
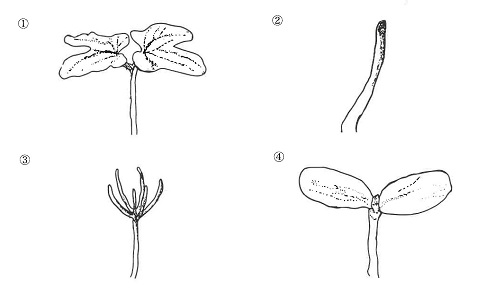
(1)次の①~④の図は,植物の子葉を描いたものです。植物の名前の組み合わせとして正しいものはどれですか。あとの(ア)~(エ)の中から1つ選び,記号で答えなさい。ただし,図の大きさの関係は実際とは異なります。
| ① | ② | ③ | ④ | |
| (ア) | アサガオ | マツ | イネ | ヒマワリ |
| (イ) | アサガオ | イネ | マツ | ヒマワリ |
| (ウ) | ヒマワリ | マツ | イネ | アサガオ |
| (エ) | ヒマワリ | イネ | マツ | アサガオ |
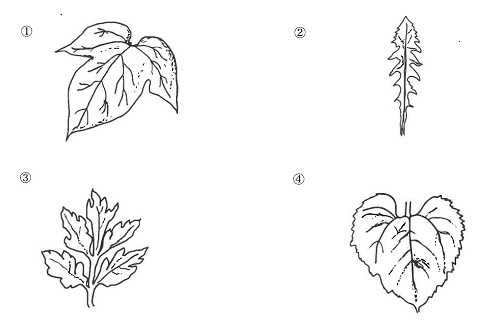
(2)次の①~④の図は,植物の本葉を描いたものです。植物の名前の組み合わせとして正しいものはどれですか。あとの(ア)~(エ)の中から1つ選び,記号で答えなさい。ただし,図の大きさの関係は実際とは異なります。
| ① | ② | ③ | ④ | |
| (ア) | アサガオ | タンポポ | ヨモギ | ヒマワリ |
| (イ) | アサガオ | ヨモギ | タンポポ | ヒマワリ |
| (ウ) | ヒマワリ | タンポポ | ヨモギ | アサガオ |
| (エ) | ヒマワリ | ヨモギ | タンポポ | アサガオ |
(3) 植物は光合成でできた栄養分からデンプンをつくります。これについて,次の(a)・(b)の問いに答えなさい。
(a)デンプンは水に溶けにくいため,植物はデンプンを分解した状態で葉からさまざまな場所に運びます。分解されたデンプンが茎の中を移動するときに通る場所の名前を答えなさい。
(b) 植物がデンプンを貯蔵している場所は,植物によって異なります。ジャガイモ,サツマイモ,イネ,バナナは,それぞれデンプンを主にどの場所に貯蔵していますか。その組み合わせとして正しいものを,次の(ア)~(カ)の中から1つ選び,記号で答えなさい。
| ジャガイモ | サツマイモ | イネ | バナナ | |
| (ア) | 茎 | 根 | 胚 | 果実 |
| (イ) | 茎 | 根 | 胚乳 | 果実 |
| (ウ) | 葉 | 根 | 葉 | 根 |
| (エ) | 葉 | 根 | 胚 | 根 |
| (オ) | 根 | 茎 | 胚乳 | 果実 |
| (カ) | 根 | 茎 | 根 | 根 |
(4)植物には,野菜や果物として食用のために育てられているものがあります。ハス,ニンジン,ピーマン,ブロッコリーでは,それぞれ主にどの部分が食用にされていますか。その組み合わせとして最も適したものを,次の(ア)~(カ)の中から1つ選び,記号で答えなさい。
| ハス | ニンジン | ピーマン | ブロッコリー | |
| (ア) | 茎 | 根 | 果実 | 花と茎 |
| (イ) | 茎 | 茎 | 根 | 花と茎 |
| (ウ) | 茎 | 果実 | 果実 | 葉と茎 |
| (エ) | 根 | 根 | 根 | 葉と茎 |
| (オ) | 根 | 茎 | 果実 | 葉 |
| (カ) | 根 | 果実 | 根 | 茎 |
(5) 野菜や果物の中には,土に埋めると芽を出すものがあります。芽は,種子から出るものもありますが,種子以外の部分である葉や茎から出るものもあります。
スーパーで買ってきたジャガイモ,タマネギ,トマト,モモを土に埋めたら,すべての野菜や果物から芽が出てきました。このとき,種子から芽が出てきたと考えられる植物の組み合わせはどれですか。次の(ア)~(カ)の中から1つ選び,記号で答えなさい。
(ア) ジャガイモ・タマネギ (イ) ジャガイモ・トマト
(ウ) ジャガイモ・モモ (エ) タマネギ・トマト
(オ) タマネギ・モモ (カ) トマト・モモ
(6)種子を発芽させてしばらく育ててから収穫する野菜として,モヤシや豆苗,カイワレ大根などがあります。豆苗やカイワレ大根には緑色の葉がついていますが,モヤシは葉がついている場合も緑色になっていません。このような違いが生じるのは,モヤシの育て方にどのような工夫をしているからですか。簡単に答えなさい。
(7) オオカナダモを使って光合成の実験をおこないました。これについて,次の(a)~(c)の問いに答えなさい。
(a) オオカナダモはどれですか。次の(ア)~(エ)の中から1つ選び,記号で答えなさい。ただし,図の大きさの関係は実際とは異なります。

(b)オオカナダモの葉を顕微鏡で観察しました。このとき,観察のしかたとして正しいものを次の(ア)~(カ)の中から1つ選び,記号で答えなさい。
(ア)オオカナダモの葉は十分に薄いので,そのままプレパラートを作成することができる。
(イ)プレパラートを作成するときは,試料をカバーガラスにのせたあと,スライドガラスをのせる。
(ウ)対物レンズは,低倍率のものよりも高倍率のものを先に使う。
(エ)顕微鏡の視野の中で右上に見えているものを中央に移動させたい場合,プレパラートは右下に移動させる。
(オ)顕微鏡の視野の中で右上に見えているものを中央に移動させたい場合,プレパラートは左下に移動させる。
(カ)接限レンズから目を離し,プレパラートと対物レンズをぎりぎりまで近づけるとピントが合う。
(c)明るい場所で育てたオオカナダモの葉を顕微鏡で観察したら,たくさんの細胞があり,それらの中には,緑色の小さな粒がたくさん見えました。次に,このオオカナダモの葉をヨウ素液につけてから顕微鏡で観察しました。このときのようすとして最も適したものを,次の(ア)~(オ)の中から1つ選び,記号で答えなさい。
(ア)細胞の周囲の部分が青紫色にに染まっていた。
(イ)細胞の内側の全部が青紫色に染まっていた。
(ウ)細胞の内側の,緑色の小さな粒が青紫色に染まっていた。
(エ)細胞の内側の,緑色の小さな粒以外の部分が青紫色に染まっていた。
(オ)青紫色に染まっていた部分はなかった。
【解説と解答】
(1)① アサガオ ② イネ ③ マツ ④ ヒマワリです。イネは単子葉、マツは多子葉です。
(答え)イ
(2) ① アサガオ ② タンポポ ③ ヨモギ ④ ヒマワリです。
(答え)ア
(3) デンプンが移動するのは師管。ジャガイモは茎、サツマイモは根、イネは胚乳、バナナは果実ですからイ。
(答え)(a) 師管 (b) イ
(4)ハスは茎、ニンジンは根、ピーマンは果実、ブロッコリーは花と茎の部分を食べます。
(答え)ア
(5) ジャガイモは茎、タマネギは葉。
(答え)カ
(6) 緑色になっていないので、光合成をさせないようにした結果です。
(答え)光をあてずに育てる。
(7) オオカナダモはエ。観察の仕方として正しいものはア。イはカバーガラスとスライドガラスが逆。ウは低倍率から始める。エ、オは右上に見えるものは右上に動かします。ピントを合わせるためにまず、対物レンズを下に下げて、そこから上げていきます。(c)葉緑体が染まります。
(答え)(a) エ (b) ア (c) ウ
【NEW!】フリーダム進学教室からのお知らせ
2020夏期講習のご案内
2020 合格手帳夏休み特集号を差し上げています。
無料です。
2020 合格手帳夏休み特集号申し込み【5年生用】
2020 合格手帳夏休み特集号申し込み【6年生用】
受験で子どもと普通に幸せになる方法、本日の記事は
4年生以下は無理しない
6年生の教室から
対立する考え
算数オンライン塾
7月12日の問題
4年生の保護者のみなさまへ中学受験パパママ塾「ONE」のご案内
【塾でのご利用について】
フリーダム進学教室 WEB学習システムOEMのご案内