2020年女子学院の問題です。
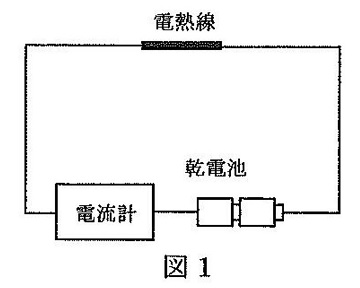
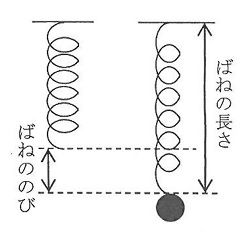
3種類の重さが無視できる軽いばねA、B、Cがある。これらのばねをそれぞれ天井につるし、30gのおもりを1個ずつつるしていったときのばねの長さを測定したところ、下の表のような結果になった。また、表からグラフ1~3を作った。ばねの長さ、ばねののびとは図に示したものである。おもりの重さをさらに増やしていったときも、おもりの重さとばねののびの関係は変わらないものとする。
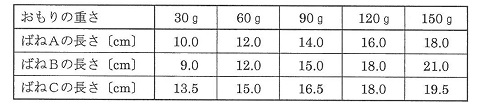
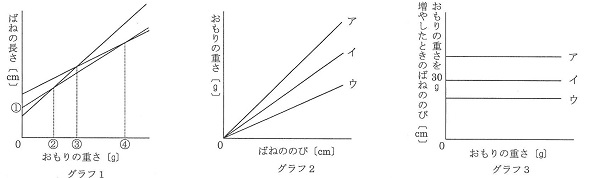
1 グラフ1の①~④の値を答えなさい。
2 グラフ2、3のア~ウは、それぞればねA、B、Cのどれですか。
3 ばねAを1cmのばすのに必要なおもりの重さを答えなさい。
4 ばねA、B、Cについて、ばねがかたい順に書きなさい。
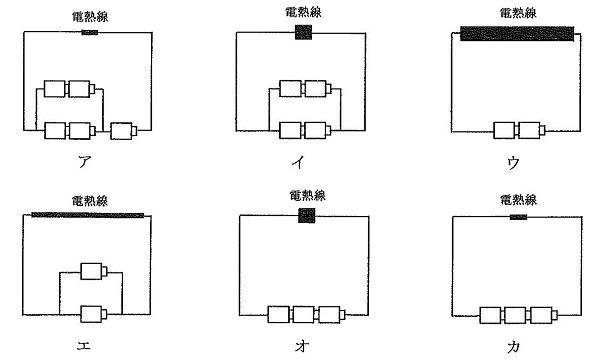
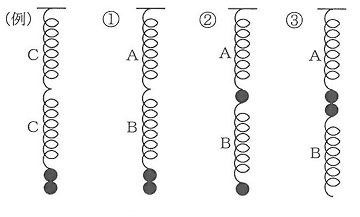
5 ばね2本と30gのおもり2個を図のようにして静止させた。(例)のときのばねC2本の長さの和は30.0cmであった。①~③のばねAとBの長さの和をそれぞれ求めなさい。
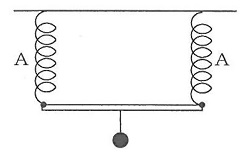
6 重さが無視できる軽い棒の両端にそれぞればねAを取り付け、図のように天井からつるした。棒の真ん中に30gのおもりを1個つるしたときのばねの長さを求めなさい。
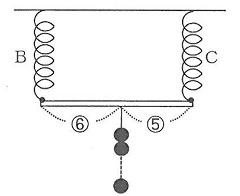
7 重さが無視できる軽い棒の両端にばねBとCを取り付け、図のように天井からつるした。棒の真ん中に30gのおもりを何個かつるしたところ、2本のばねの長さは等しくなり棒は水平になった。
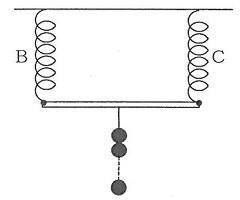
(1)このときの、ばねの長さとおもりの重さを求めなさい。
(2)おもりをつるす位置は変えずに、おもりの重さを増やしたところ、棒は水平ではなくなった。棒は左右どちらが下がりますか。
(3)おもりの重さを600gにして、ばねBとCの長さが等しくなり棒を水平にするためには、おもりはどの位置につるせばよいか。【棒の左端からおもりをつるす位置までの長さ】と【おもりをつるす位置から棒の右端までの長さ】の比を、最も簡単な整数の比で答えなさい。
8 重さが無視できる軽い棒の両端にばねBとCを取り付け、図のように棒の左端から6:5の位置に30gのおもりを何個かつるしたところ、2本のばねの長さは等しくなり棒は水平になった。このときの、ばねの長さとおもりの重さを求めなさい。
【解説と解答】
1
Aば30gで2cm、Bは30gで3cm、Cは30gで1.5cmですから、グラフ1の0gのときの位置(自然長)が上からC、A、Bの順になります。したがって①はAの自然長になるので、10.0-2.0=8.0cm。②はBがAに追いつくところなので、Bの自然長は6.0cmですから、自然長の差2.0cmを30gについて3-2=1.0cmで追いかけるから30×(2÷1)=60g
③はBがCに追いつくところなので、自然長の差が12.0-6.0=6.0 30gについて3.0-1.5=1.5cm追いつくので
6.0÷1.5×30=120g。
④はAがCに追いつくところなので、自然長の差が12.0-8.0=4.0で30gについて2.0-1.5=0.5cm追いつくので
4÷0.5×30=240g
(答え)① 8.0cm ② 60g ③ 120g ④ 240g
2
グラフ2は同じ伸びを得るのに必要な重さのグラフだから、アがC、イがA、ウがB。
グラフ3は30gあたりの伸びを示すのでアがB、イがA、ウがC。
(答え)グラフ2 ア C、イ A、ウ B グラフ3 ア B、イ A、ウ C
3 ばねAは30gで2cm伸びるので1cmのビルのには15g
(答え)15g
4 かたい順というのは、同じ重さでのびない順なので、CAB
(答え)CAB
5 ①はAにもBにも60gかかるので、12.0×2=24.0cm
②はAには60g、Bには30gかかるので、12.0+9.0=21.0cm
③はAには60g、Bには0gなので、12.0+6.0=18.0cm
(答え)①24.0cm ② 21.0cm ③ 18.0cm
6 それぞれ15gかかるので1cmずつ伸びます。Aの自然長は8.0cmなので、8.0+1.0=9.0
(答え)9.0cm
7
(1) BとCが同じ長さになるのは120gの重さをかけたときで、その長さは18.0cmです。
120×2=240g。
(答え)18.0cm 240g
(2)同じ重さをかけたら、Bの方がのびるので、左側は下がります。
(答え)左
(3)BとCが同じ長さになるのは240gで、その後のびの比はB:C=2:1になるので、かかる重さの比を1:2にすれば同じ長さを保つことができます。
360÷(1+2)×1=120gからBには120+120=240g、Cには600-240=360gかければよいので、240:360=2:3から3:2
(答え)3:2
8
左から6:5の位置におもりをつるすとBには【5】、Cには【6】の重さがかかります。
【5】-120:【6】ー120=1:2 【6】-120=【10】ー240 【4】=120 【1】=30g
よっておもりの重さは30×11=330g
Bにかかる重さは150gなので、21cm
(答え)21cm 330g

【NEW!】フリーダム進学教室からのお知らせ
2020 合格手帳4ー6月号を差し上げています。
無料です。
2020合格手帳4ー6月号申し込み【5年生用】
2020合格手帳4ー6月号申し込み【6年生用】
中学受験で子どもと普通に幸せになる方法、本日の記事は
オンラインの方が楽?
6年生の教室から
全てを見通せる
慶應進学館から
面接の意味
4年生の保護者のみなさまへ中学受験パパママ塾「ONE」のご案内


【塾でのご利用について】
フリーダム進学教室 WEB学習システムOEMのご案内

にほんブログ村