2017女子学院の問題です。
小さい鉄球を使って、[実験1】~【実験3】を行った。
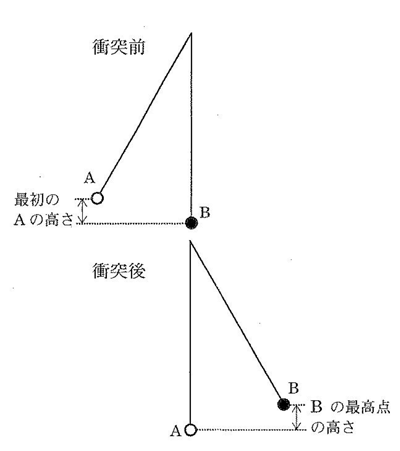
【実験1】図のように、ともに30gの鉄球A、Bにそれぞれ同じ長さの丈夫でのびない糸をつけ、同じところからつり下げた。Bは静止させ、Aを糸がたるまないように持ち上げて放したところ、AはBと衝突して静止し、Bは糸がたるまずに上がっていった。
最初のAの高さを変えて何回か同じように実験をしたところ、いずれも最初のAの高さと衝突後のBの最高点の高さは等しかった。
【実験2】30gの鉄球Bのかわりに90gの鉄球Cを使って、実験1と同じ実験をしたところ、A、Cは衝突した後、互いに逆向きに同じ速さで進みはじめ、再び衝突した。
1 ふりこの動きにはきまりがある。ふりこが1往復する時間は何によって決まるか、次のア~ウから選びなさい。
ア おもりの重さ イ 最初のおもりの高さ ウ 糸の長さ
2 実験1、2の結果から、次の①と②の関係について、正しいものをあとのア~エからそれぞれ選びなさい。
(1)①「Aが動き始めてからBに衝突するまでの時間」と、②「BがAと衝突してから最高点に達するまでの時間」
(2)①「Bに衝突する直前のAの速さ」と、②「Aと衝突した直後のBの速さ」
(3)①「BがAと衝突してから最高点に達するまでの時間」と、②「CがAと衝突してから最高点に達するまでの時間」
(4)①「最初のAの高さ」と、②「衝突後のCの最高点の高さ」
(5)①「Aと衝突した直後のBの速さ」と、②「Aと衝突した直後のCの速さ」
ア ①>② イ ①=② ウ ①く② エ 決まっていない
3 実験2において、2回目の衝突の位置について、正しいものを次のア~ウから選びなさい。
ア 1回目の衝突の位置より左側 イ 1回目の衝突の位置と同じ ウ 1回目の衝突の位置より右側
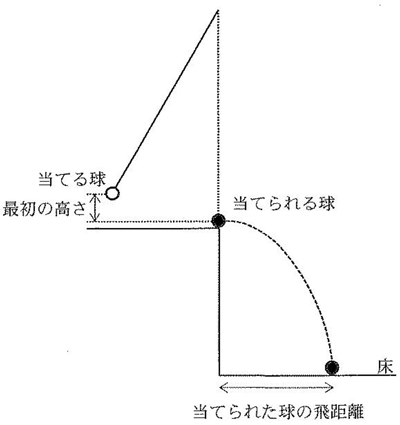
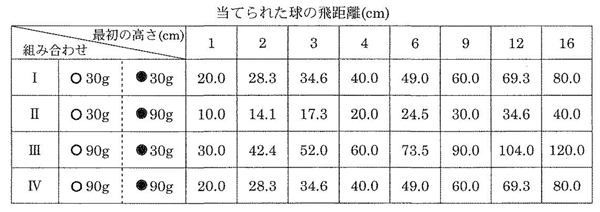
【実験3】 図のように、段差の上に糸のついていない鉄球(当てられる球●)を置き、糸のついている鉄球(当てる球○)を持ち上げ手を放すと、2コの球は衝突し、当てられた球(●)は床に落下した。この実験を、鉄球の組み合わせと最初の高さを変えて行い、当てられた球の飛距離を測定したところ、下の表のような結果になった。
4 実験3の結果から考えて、正しいものには〇、間違っているものにはXを書きなさい。
(1)当てる球の最初の高さ、当てる球の重さが同じ場合、当てられる球の重さを3倍にすると、飛距離は半分になる。
(2)当てる球の最初の高さ、当てられる球の重さが同じ場合、当てる球を重くすると、飛距離は大きくなる。
(3)当てる球と当てられる球の重さが同じ場合、球の重さによって、飛距離は変わらない。
(4)当てる球の最初の高さを4倍にすると飛距離は2倍になり、当てる球の最初の高さを9倍にすると飛距離は4.5倍になる。
5 当てられた球の飛距離が110~130cmになる〔鉄球の組み合わせ,最初の高さ〕を次のア~エからすべて選びなさい。
ア 〔I,36cm〕 イ 〔Ⅱ,36cm〕 ウ 〔Ⅲ,18cm〕 エ 〔Ⅳ,27cm〕
【解説と解答】
1 ふりこの周期はふりこの長さで決まります。
(答え)ウ
2
(1)Aが動き始めてからBに衝突するまでの時間=BがAと衝突してから最高点に達するまでの時間
(2)Bに衝突する直前のAの速さ=Aと衝突した直後のBの速さ
(3)BがAと衝突してから最高点に達するまでの時間=CがAと衝突してから最高点に達するまでの時間
(4)最初のAの高さ>衝突後のCの最高点の高さ
(5)Aと衝突した直後のBの速さ>Aと衝突した直後のCの速さ
(答え)(1)イ (2)イ (3)イ (4)ア (5)ア
3 衝突する場所は同じになります。
(答え)イ
4 高さを4倍にすると、飛ぶ距離は2倍です。16倍にすると4倍になっています。●が○の3倍のとき、距離は同じ時の半分になっています。
逆に○が●の3倍の時、1.5倍になっています。
(答え)
(1)○ (2)○ (3)○ (4)×
5
ア 36cmは9cmの4倍なので、60cm×2=120cm
イ 36cmは9cmの4倍だから、30cm×2=60cm
ウ 18cmは2cmの9倍だから42.4cmの4倍
エ 27cmは3cmの9倍だから34.6cm×3=103.8cmで及びません。
(答え)ア ウ
受験で子どもと普通に幸せになる方法、本日の記事は
たのしい練習、しんどい練習
5年生の教室から
記述はとにかく答える
中学受験 算数オンライン塾
3月4日の問題