2021年サレジオ学院の問題です。
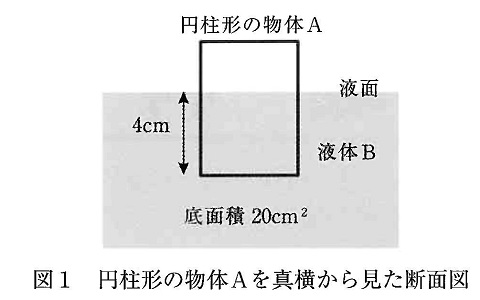
図1のように,底面積20cm2の円柱形の物体Aが液体Bに浮いています。物体Aには重力と液体による浮力がはたらいていますが,液体による浮力の大きさは,次に示すアルキメデスの原理を用いて求めることができます。
アルキメデスの原理
「液体中にある物体は,その物体が押しのけた液体の重さに等しい大きさの浮力を受ける」
液体Bは1cm3あたり1.5gであり,物体Aの底面はつねに液面に平行であるとします。次の(1)~(5)の問いに答えなさい。ただし,計算結果を答える際,割り算が必要な場合は,分数ではなく小数で答えなさい。
はじめは,図1のように物体Aは底面が深さ4cmになる位置で静止しました。
(1)物体Aが押しのけた液体Bの体積は何cm3ですか。
(2)物体Aが押しのけた液体Bの重さは何gですか。
(3)物体Aの重さは何gですか。
次に、図1と同じ物体Aに糸をつけ,図2のように糸を定かっ車に通して糸の端におもりCをつるすと,物体Aは,底面が深さ2.5cmになる位置で静止しました。ここで,糸の重さや糸とかっ車の間のまさつは考えないものとします。
(4)おもりCの重さは何gですか。
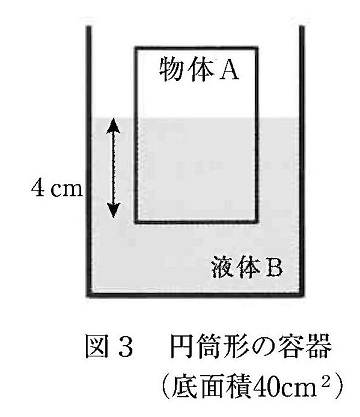
こんどは,図3のように容器内側の底面積が40cm2の円筒形の容器に液体Bを入れ,物体Aを液体Bの中に入れると,図1と同じように,物体Aは底面が深さ4cmになる位置で静止しました。続いて,物体Aを手で止めて図2と同じように,物体Aに糸をつけて定かっ車に通して糸の端に90gのおもりDをつるします。
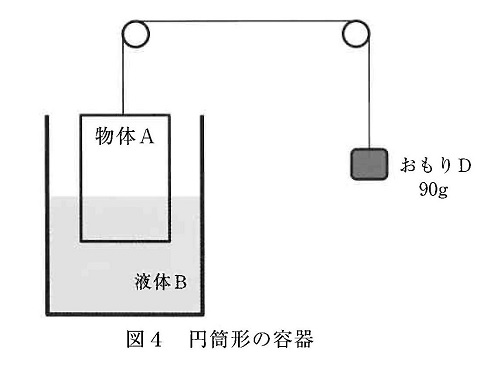
最後に,物体Aから手をはなすと,はじめ物体Aと液面は上下に動きますが,やがて図4のように物体Aと液面は静止します。
(5)物体Aが静止した位置は手をはなした位置よりも何cm高いですか。
【解説と解答】
(1)Aの底面積は20cm2で、深さ4cmですから20×4=80cm3を押しのけています。
(答え)80cm3
(2)液体Bの比重が1.5ですから1.5×80=120gです。
(答え)120g
(3)浮力が120gですから、物体Aの重さも120gです。
(答え)120g
(4)物体Aが受けている浮力は20×2.5×1.5=75gですから、45g軽くなりました。
したがっておもりCの重さが45gです。
(答え)45g
(5)物体Aにかかる重さは120-90=30gですから、押しのける体積は30÷1.5=20cm3です。
20cm3増えるので、液面の高さは20÷40=0.5cm高くなります。さらに
20÷20=1cm分物体Aは物体Bから浮くので、合計0.5+1=1.5cm高くなります。
(答え)1.5cm
今後、投稿のタイミングを定時以外に増やしていきます。投稿のタイミングをTwitterでお知らせしていますので、ぜひフォローしてください。
田中貴のTwitter
Newフリーダムオンラインからのお知らせ
フリーダムオンライン 冬期講習のお知らせ
New
合格手帳の9-11月号ができました。秋に向けてしっかり計画を立てていきましょう。
2021 合格手帳 5年生用9-11月号のお知らせ
受験で子どもと普通に幸せになる方法、本日の記事は
親は何をするかをまとめてみる
【塾でのご利用について】
フリーダム進学教室 WEB学習システムOEMのご案内