立教新座中学の問題です。
図のような台形ABCDがあります。辺BC上に2点、E、Fを三角形ABEと三角形DFCがともに直角三角形になるようにとったところ、BFとEFの長さが同じになりました。また、AEとDFの交点をGとします。BFとFCの長さの比が3:4、三角形ABFの面積が36cm2のとき、次の問いに答えなさい。
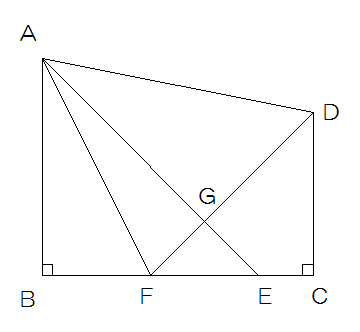
(1)CEの長さを求めなさい。
(2)DGとGFの長さの比を求めなさい。
(3)三角形AGDの面積を求めなさい。
(解説と解答)
(1)
BFとFEの長さが同じになり、BF:FC=3:4であるので、BF:FE:EC=3:3:1になります。
したがってBF=【3】とすると、AB=【6】、CD=【4】三角形ABFの面積は【6】×【3】÷2=36cm2 【1】×【1】=4cm2 より【1】=2cm
CE=2cm
(答え)2cm
(2)
下図でFからABに平行に線を引き、AGとの交点をH、EからABに平行に線を引きGDとの交点をIとします。
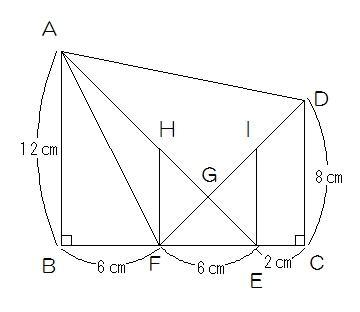
このとき三角形HFEも三角形IEFもともにFE=6cmの直角二等辺三角形ですから。FG:GI=1:1
またFI:ID=3:1よりFG:GI:ID=3:3:2からDG:GF=5:3
(答え)5:3
(3)三角形AFDの面積は台形ABCDから三角形ABFと三角形FCDを引けばよいので
(12+8)×14÷2-12×6÷2-8×8÷2=140-36-32=72cm2
FG:GD=3:5より三角形AGD=72÷(3+5)×5=45cm2
(答え)45cm2
「映像教材、これでわかる比と図形」(田中貴)
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
うまくいかないときだってある
==============================================================
中学受験 算数オンライン塾
8月5日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

