2017年東邦大東邦の問題です。
図のような長方形ABCDにおいて,辺ADを3等分する点をE,Fとします。 また,ACとBDの交点をG, ACとBFの交点をH,BDとCFの交点をIとします。
このとき,次の問いに答えなさい。
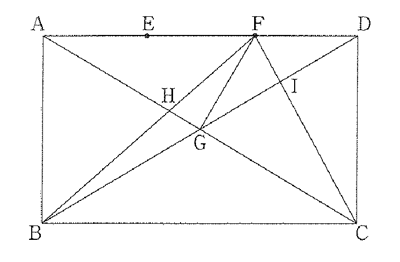
(1)(AHの長さ)と(HGの長さ)の比を最も簡単な整数で表しなさい。
(2)(三角形AGFの面積)と(三角形BGHの面積)の比を最も簡単な整数で表しなさい。
(3)(三角形CIGの面積と三角形DFIの面積の差)と(三角形BGHの面積)の比を 最も簡単な整数で表しなさい。
【解説と解答】
(1)AH:HC=2:3 AG:GC=1:1よりAH:HG:GC=4:1:5
(答え)4:1
(2)三角形AGFの底辺を【2】、高さを(1)とすると三角形BGCの底辺は【3】、高さは(1)となり面積比は2:3 三角形BGH:三角形BGC=1;5より
三角形AGF:三角形BGH=10:3
(答え)10:3
(3)三角形CIGと三角形DFIの差は三角形GCFと三角形FGDとの差に等しい。
三角形GCFは長方形ABCDの6分の1、三角形FGDは長方形ABCDの12分の1に等しいのでその差は12分の1。三角形BGHは長方形ABCDの2分の1の10分の1だから20分の1になるので、求める比は5:3
(答え)5:3
受験で子どもと普通に幸せになる方法、本日の記事は
時空を飛ぶ塾
5年生の教室から
第一志望を決める
今日の慶應義塾進学情報
ます基礎力




