2015年早稲田実業の問題です。
大きな紙にAB=4cm、BC=8cmの長方形ABCDをかきました。この紙に次の点Pの取り方にしたがって点Pをとります。
点Pの取り方
三角形PAB、三角形PBC、三角形PCD、三角形PADの4つの三角形のなかには、面積が6㎝2の三角形と面積が8cm2の三角形がある。
(1) 図1のように点Pをとったとき,三角形PABの面積が8cm2になりました。このとき、三角形PBCの面積を求めなさい。

(2)長方形ABCの内部(図2の影の部分)に点Pの取り方にしたがってとれる点は、全部で何個ありますか。
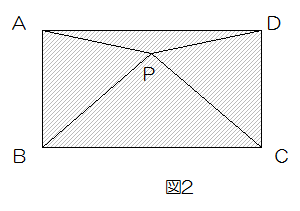
(3)点Pの取り方にしたがってとれる点は、全部で何個ありますか。
【解説と解答】
(1) 三角形PABと三角形PCDの面積の和は4×8÷2=16cm2です。三角形PABが8cm2であれば、三角形PCDも8cm2になるので、三角形PADが6㎝2になるから、
4×8+6-8×2=38-16=22cm2になります。
(答え)22cm2
(2) 三角形PABと三角形PDCの和が16cm2、三角形PADと三角形PBCの面積の和も16cm2です。
三角形PAB=8cm2のとき、三角形PDCの面積は8cm2と決まるので、三角形PADと三角形PBCの面積はどちらかが6cm2、どちらかが10㎝2なので、2通り。
三角形PAB=6cm2のとき、三角形形PDCの面積は10cm2と決まるので、三角形PADと三角形PBCの面積はどちらも8cm2。
三角形PAB=10cm2のとき、三角形形PDCの面積は6cm2と決まるので、三角形PADと三角形PBCの面積はどちらも8cm2。
したがって4通りになります。
(答え)4通り
(3)
(2)でPが長方形の内側にあるのは4通り。外側にある場合を下図のように考えます。
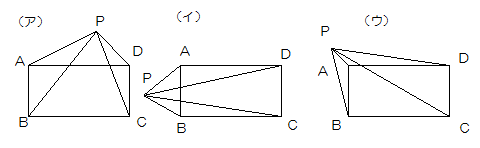
(ア)の場合、Pは横の位置が直線ABと直線CDの間に来るので、三角形ABPと三角形PDCの和が16cm2になるので、三角形PABが8cm2であれば、三角形PDCも8cm2になるので、三角形PADが三角形PBCが6㎝2になるから2通り。
三角形PAB=6㎝2であれば、三角形PDC=10cm2、三角形PADか三角形PBCのどちらかが8cm2になるので、4通り。合計6通り。
(イ)の場合、Pは縦の位置が直線ADと直線BCの間に来るので、三角形APDと三角形PBCの和が16cm2になるのから、(ア)と同じように6通り。
(ウ)の場合、三角形PADと三角形PAB、三角形PABと三角形PBC、三角形PBCと三角形PDC、三角形PDCと三角形PADのどちらかかが8cm2、どちらかが6㎝2になるので、2×4=8通り。
したがって合計4+6+6+8=24通りになります。
(答え)24通り
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
とにかく式を書く
==============================================================
今日の慶應義塾進学情報
付属校から他大学を受ける
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

