2015年筑波大駒場の問題です。
縦100個、横100個、全部で10000個のます目が書かれた表があります。表のそれぞれのます目には、次のように整数が1つずつ書かれています。
1行目には、すべて1が書かれています。
2行目には、1から1ずつ増える数が100個、順に書かれています。
3行目には、1から2ずつ増える数が100個、順に書かれています。
4行目には、1から3ずつ増える数が100個、順に書かれています。
・・・・・
99行目には、1から98ずつ増える数が100個、順に書かれています。
100行目には、1から99ずつ増える数が100個、順に書かれています。
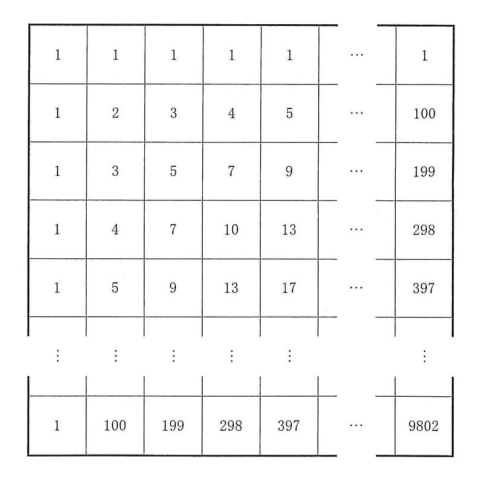
次の問いに答えなさい。
(1)この表に、100は全部で何個書かれていますか。
(2)この表に、ちょうど5個書かれている整数があります。そのような数のうち、最も小さいものを答えなさい。
(3)100から200までの整数のうち、この表にちょうど1個書かれている数をすべて答えなさい。
【解説と解答】
(1)1から順に増えていくので100は99増えれば良いことになります。
99を素因数分解すると3×3×11ですから、1ずつ増える、3ずつ増える、9ずつ増える、11ずつ増える、33ずつ増える、99ずつ増えるの6つの場合があります。
(答え)6個
(2)その数から1を引いたとき、1を含めて5つの約数が存在すればいいので、2×2×2×2が一番小さくなります。したがって1+2×2×2×2=17
(答え)17
(3)100以上の数ですから、上から2段目までには出てきません。
すると例えば102は1引くと101になり、これは素数ですから約数がありません。しかし101ずつ増える段はこの表にはないので、存在しないことになります。
したがって約数はなければなりません。
素因数分解したとき二つの数の積で表される場合を考えます。例えば11×11の場合は11ずつふえる段の12番目に出てます。これは1つだけです。
しかし11×13は11ずつ増える14番目と13ずつ増える12番目に出てくるので、2つになってしまいます。
ということは、二つの積で表せ、かつ平方数であるということが求められます。
100から200までの数でその数は11×11、13×13の2つだけです。
したがって求める数は121+1=122 169+1=170です。
(答え)122 170
「映像教材、これでわかる数の問題」(田中貴)
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
成績が落ちたとき
==============================================================
今日の慶應義塾進学情報
男子の3校狙い
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

