2016年早稲田高等学院の問題です。
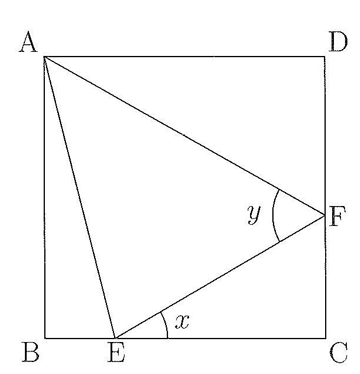
図のように、正方形ABCDの辺BC、CD上にそれぞれ点E、Fをとるとき、次の問いに答えなさい。
(1)角BAEが17°、角DAFが28°であるとします。このとき、図の中の角xと角yの大きさを、それぞれ求めなさい。
(2)角AECと角AFCの和が225°、三角形ECFの面積が正方形ABCDの面積の$$\frac{4}{25}$$倍であるとします。このとき三角形AEFの面積は三角形ECFの面積の何倍か求めなさい。
【解説と解答】
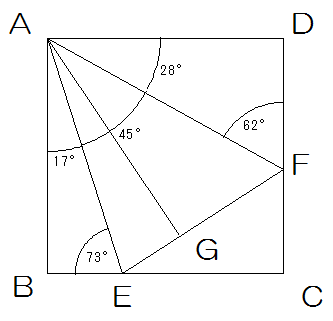
(1)図のAE、AFで折り返すとADとABはAGEに重なります。したがって
x=180-73×2=34° y=62°
(答え)x=34° y=62°
(2)角EAFは同じく45°ということになりますから、(1)と変わらず、図のAE、AFで折り返すとADとABはAGEに重なります
三角形AEFは全体の1-$$\frac{4}{25}$$=$$\frac{21}{25}$$の半分になります。
したがって$$\frac{21}{50}$$÷$$\frac{4}{25}$$=2$$\frac{5}{8}$$
(答え)2$$\frac{5}{8}$$倍
受験で子どもと普通に幸せになる方法、本日の記事は
中学受験 算数オンライン塾