2016年筑波大駒場中学の問題です。
正三角形ABCの辺上に点DEがあり、ADとDBの長さの比は3:2、AEとECの長さの比は2:3です。また点Pは次の(1)(2)(3)のように正三角形ABCの内側にあります。正三角形ABCの面積が100cm2のとき、三角形PBCの面積を求めなさい。
(1)PはDE上にあり、DPとPEの長さの比は9:1
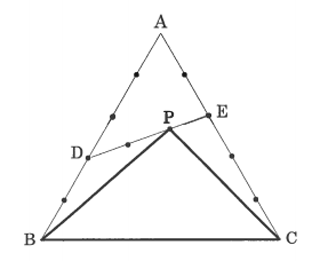
(2)Fは辺AB上にあり、AF:FBの長さの比は1:4
Gは辺AC上にあり、AGとGCの長さの比は4:1
PはDEとFGが交わった点
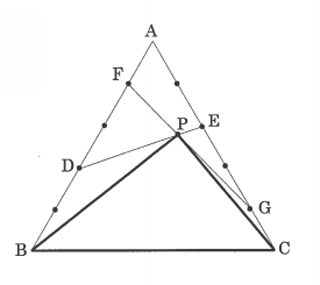
(3)PDとAB、PEとACはそれぞれ垂直。
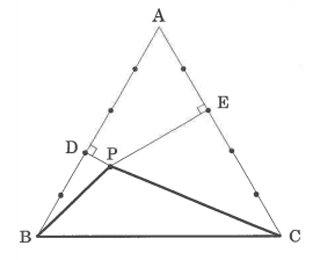
【解説と解答】
(1)三角形ADE=$$\frac{3}{5}$$×$$\frac{2}{5}$$=$$\frac{6}{25}$$
三角形PEC=$$\frac{3}{5}$$×$$\frac{3}{5}$$×$$\frac{1}{3}$$=$$\frac{3}{25}$$
三角形PDB=$$\frac{2}{5}$$×$$\frac{2}{5}$$×$$\frac{2}{3}$$=$$\frac{8}{75}$$
三角形PBC=1-=$$\frac{6}{25}$$ー$$\frac{3}{25}$$ー$$\frac{8}{75}$$=$$\frac{8}{15}$$
100×$$\frac{8}{15}$$=53 $$\frac{1}{3}$$
(答え)53 $$\frac{1}{3}$$cm2
(2)
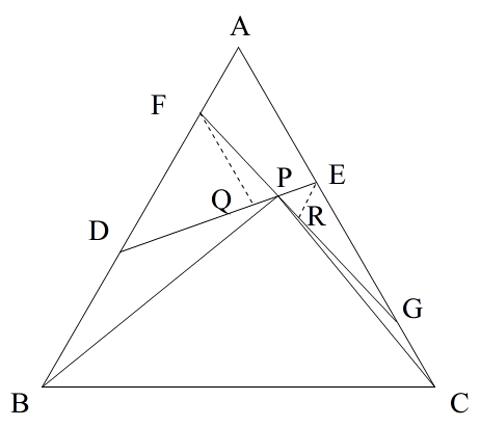
図のようにFかACに平行に線を引き、DEとの交点をQとします。AE=【2】とすると、AF:FD=1:2よりFQ=【$$\frac{4}{3}$$】EG=【2】より FP:PG=2:3
三角形DPB=$$\frac{4}{5}$$×$$\frac{4}{5}$$×$$\frac{2}{5}$$×$$\frac{1}{2}$$=$$\frac{16}{125}$$
同様にEからABに平行に線を引き、FGとの交点をRとするとAF=【1】 AE:EG=1:1よりER=【$$\frac{1}{2}$$】FD=【2】よりDP:PE=4:1
三角形PEC=$$\frac{3}{5}$$×$$\frac{3}{5}$$×$$\frac{1}{5}$$=$$\frac{9}{125}$$
三角形ADE=$$\frac{3}{5}$$×$$\frac{2}{5}$$=$$\frac{6}{25}$$
1-$$\frac{6}{25}$$ー$$\frac{16}{125}$$ー$$\frac{9}{125}$$=$$\frac{14}{25}$$
100×$$\frac{14}{25}$$=56
(答え)56cm2
(3)
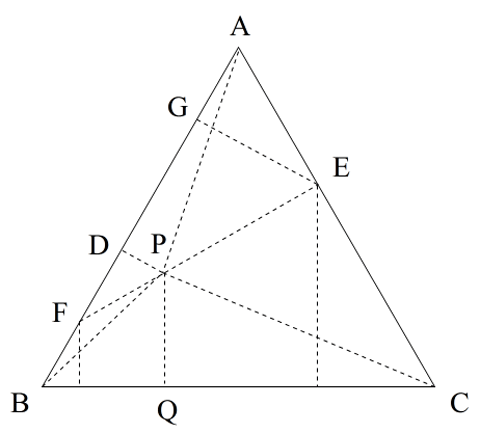
図でEPをまっすぐ伸ばしたとき、ABとの交点はDBの中点になります。三角形GFEも三角形AGEも正三角形の半分の直角三角形になっているからです。
FD:DG=1:2 GE=(3)とするとDP=(1) FE=(6) FP=(2) PE=(4)
EからBCに下ろした垂線の長さを<3>とすれば、FからBCに下ろした垂線の長さは<1> その差<2>を1:2に分けるので、PQの長さは<1>+<2>×$$\frac{1}{3}$$=<$$\frac{5}{3}$$>
したがってQPは正三角形ABCの高さ<5>のちょうど$$\frac{1}{3}$$になるから面積も$$\frac{1}{3}$$。
100×$$\frac{1}{3}$$=33 $$\frac{1}{3}$$
(答え)33 $$\frac{1}{3}$$
============================================================
受験で子どもと普通に幸せになる方法、本日の記事は
できるだけ解けばよい
==============================================================
今日の慶應義塾進学情報
慶應中等部説明会日程
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

