2015年聖光学院の問題です。
袋の中に赤玉、白玉、青玉がそれぞれ何個かずつ入っています。 これを小さい箱ですくって、A、B、C、Dの4人に1杯ずつ配り、残った玉をEに渡したところ、5人とも持っている玉の個数が同じでした。また、Aが持っている白玉の個数は最初に袋に入っていた玉の総数の40分の1でした。
その後、CがBに赤玉を32個渡し、DがBに赤玉を80個渡し、DがEに青玉を56個渡すと、それぞれが持っている赤玉と白玉と青玉の個数の比は5人とも同じになりました。
また、CとDが持っている玉の個数の合計は、Eが持っている玉の個数の合計より32個多くなっていました。
このとき、次の問いに答えなさい。
(1)最初に袋の中に入っていた玉の総数は何個ですか。
(2)Eが最後に持っていた白玉の個数は何個ですか。
(3)最初に袋の中に入っていた玉の中で青玉の個数が1番多いとき、最初に袋の中に入っていた赤玉と白玉と青玉の個数の比を最も簡単な整数比で答えなさい。
【解説と解答】
(1)最初の条件から次の表が得られます。
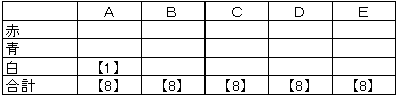 表1
表1
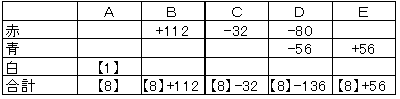 表2
表2
表2からCとDの持っている合計は【16】-32-136=【8】+56+32
より【8】=32+136+56+32=256個
したがって全体の個数は256×5=1280
(答え)1280個
(2)Aは最後に256個、Bは256+112=368個、Cは256-32=224個
Dは256-136=120個 Eは256+56=312個です。
Aの白玉は全体の40分の1ですから、1280÷40=32個 したがって白玉は各自が持つ玉の総数の8分の1になります。
その割合は同じなので、Eは312÷8=39個白玉があったことになります。
(答え)39個
(3)みんな赤、白、青の比は同じになり、白は全体の8分の1とわかっています。
またそれぞれの8分の1の数である32、46、18、15、39は1以外の公約数がないので、それぞれの赤、青は白の整数倍であることがわかります。
Bの赤は112個多くなりました。ということはBの赤は112個よりは多くなりますが、それよりも青は多くなければならないということになります。
Bの青と赤の合計は368÷8×7=322個ですから、青は322÷2=161よりは大きくなります。
また赤は112よりは大きいので、322-112=210よりは小さくなります。
46の倍数で161より大きく210より小さい数は184しかありません。
したがってBの青が184個、赤が138個、白46個となるので、
赤:白:青=3:1:4と決まります。
(答え)赤:白:青=3:1:4
「映像教材、これでわかる数の問題」(田中貴)
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
解き方を覚えろ
==============================================================
今日の慶應義塾進学情報
なぜ中等部は男子の方が多いのか
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

