2018年 洗足学園第2回の問題です。
もとの長さが10cmの2種類のばねA、Bと太さが一様な長さ15smの棒Cを用意しました。図1は、ばねA、Bにつるしたおもりの重さと、ばねの伸びの関係を表しています。ただし、ばねの重さは無視できるものとします。答えは、小数第3位以下があるときは、四捨五入して4、数第2位まで答えなさい。

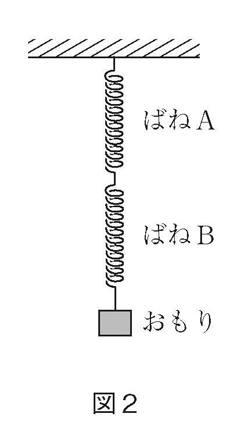
(1) 図2のようにばねA、Bをつないで60gのおもりをつるしたとき、2本のばねの長さを足すと何cmになりますか。
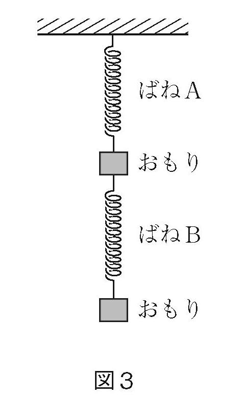
(2) 図3のように30gのおもりを2つ用意し、ばねA、おもり、ばねB、おもりの順につないだとき、2本のばねの長さを足すと何cmになりますか。
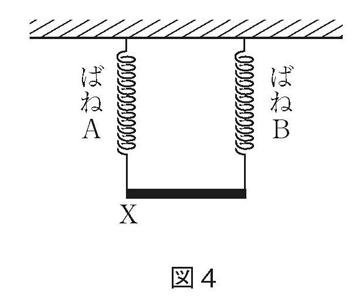
(3) 図4のようにばねA、Bに棒Cをつるしました。そこに120gのおもりをつるして棒Cが水平になるようにしました。おもりを棒Cの端Ⅹから何cmの位置につるせばよいですか。また、そのときのばねの長さは何cmになりますか。ただし、棒Cの重さは無視できるものとします。
(4)(3)で用いた棒Cの重さが60gであるとすると、(3)で得られた位置に120gのおもりをつるしたとき、ばねA、Bはそれぞれ何cmになりますか。ただし、棒Cが傾いてもばねの伸びには影響を与えないものとします。
(5) 図5のようにばねAを2つとばねBを1つ用意し、棒Cをつるしました。100gのおもりを棒Cのある位置につないだとき、すべてのばねが5cm伸びて棒Cが水平になりました。おもりを棒Cの端Ⅹから何cmの位置につるせばよいですか。ただし、棒Cの重さは無視できるものとします。
【解説と解答】
(1) 60gのおもりをかけたので、Aは12cm、Bは6cmのびるから合計18cmです。自然長がそれぞれ10cmですから、合計38cmになります。
(答え)38cm
(2)Aには60g、Bには30gかかるので、Aは12cm、Bは3cmになるから合計15cmです。自然長がそれぞれ10cmですから、合計35cmになります。
(答え)35cm
(3)ばねの伸びの比はA:B=2:1になるので、逆に1:2になるように重さが分配されれば良いことになります。
したがって長さが15cmですから、Xからは10cm。またそのとき、Aには40g Bには80gの重さがかかるので、ばねの長さは10+8=18cmです。
(答え)10cm 18cm
(4)均質な棒は真ん中に重さがかかります。Xからの回転力で考えると
10×120+7.5×60=1200+450=1650 1650÷15=110gがBにかかり、Aには120+60-110=70gかかります。
したがってAは14cm、Bは11cmになります。自然長を加えるからAは24cm、Bは21cmです。
(答え)A 24cm B 21cm
(5)ばねAとばねBの伸びの比は2:1ですから、Bに【2】、Aには【1】ずつの重さがかかるので、
【4】=60gから【1】=15gです。
Xからの回転力で考えると60×Xからの距離=15×10+15×15=375
X=6.25cm
(答え)6.25cm
フリーダム進学教室 新連載 学校訪問シリーズ
第2回 東京都市大等々力中学
受験で子どもと普通に幸せになる方法、本日の記事は
ホントにこんなことしないと受からないんですか?
5年生の教室から
最初が肝心 ー金原 崇ー
慶應進学特別から
慶應の算数、特別授業のお知らせ
自宅でできるオンライン個別指導「スタディールームオンライン」