2017年東洋英和の問題です。
地しんについて、各問いに答えなさい。
(1) 下の文のアとイに入る言葉を答えなさい。
地しんが発生した場所をしん源といい、ある地点における地しんのゆれの大きさを(ア)といいます。地しんの規模(エネルギーの大きさ)を(イ)といい、Mと表すこともあります。
(2) (1)のアとイについて正しいものを次から2つ選び、番号で答えなさい。
1 1つの地しんにおいて、アの値は1つで、イの値は観測地により異なる。
2 1つの地しんにおいて、イの値は1つで、アの値は観測地により異なる。
3 しん源からの距離が遠くなるにつれ、ふつうアの値は小さくなる。
4 しん源からの距離が同じであれば、地ばんの性質によらず、アの値は同じになる。
5 アの値は10まである。
(3)地しんが発生すると、しん源から速さの異なる2種類の波が同時に伝わっていきます。速い波をP波といい、観測地に先に到達し小さなゆれを起こします。遅い波をS波といい、観測地に遅れて到達し、大きなゆれを起こします。
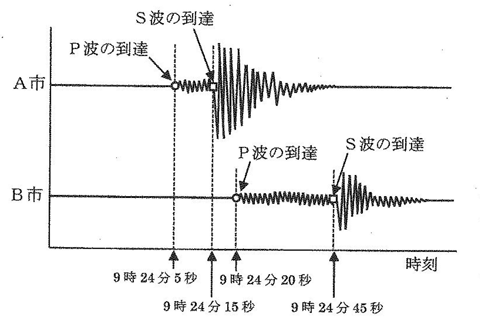
図はある地しんについて、しん源から80kmはなれたA市と、しん源から200kmはなれたB市で観測したゆれの記録を示したものです。A市では9時24分5秒にP波が到達して小さなゆれが起こり、9時24分15秒にS波が到達し大きなゆれが起きたことが分かります。
① この地しんのP波の速さは毎秒何kmですか。
② この地しんの発生時刻は9時何分何秒ですか。
(4)先に到達するP波を観測することで、その後に到達するS波による大きなゆれを事前に予測して知らせる気象庁のシステムを何というか答えなさい。
【解説と解答】
(1) アは震度、イはマグニチュードです。
(2) 震度は観測地によって違いますが、マグニチュードは1つの値に決まります。しん源地から遠くなるにつれ、震度も小さくなります。
(3) ① A市からB市までは200-80=120㎞あり,これをP波は9時24分20秒-9時24分5秒=15秒で伝わっているので、速さは毎秒120÷15=8㎞です。
② 震源からA市までは80㎞あり,これをP波は80÷8=10秒で伝わります。したがって,地震の発生時刻は,A市にP波が初めて届く10秒前の9時24分5秒-10秒=9時23分55秒です。
(4)緊急地震速報といいます。
(解答)
(1)ア 震度 イ マグニチュード
(2)2・3
(3)① 8 ② 23・55
(4)緊急地震速報
受験で子どもと普通に幸せになる方法、本日の記事は
次にできるか?
6年生の教室から
出た数字は何かをメモする
中学受験 算数オンライン塾
5月13日の問題