2017年桜蔭中学の問題です。

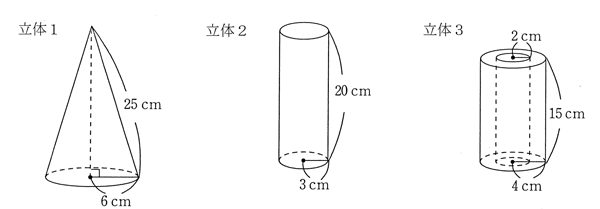
図のような立体1、2、3がどれも1個以上あります。立体1は円すい、立体2は円柱、立体3は底面の半径が4cmの円柱から底面の半径が2cmの円柱をくりぬいてできた立体です。
立体1の底面（下の面）は赤、立体2の底面（上下の2つの面）は青、立体3の底面（上下の2つの面）は黄色にぬられていて、どの立体もその他の面は全て白くぬられています。
このとき次の問いに答えなさい。
（1）立体1、2、3の1個ずつについて、白くぬられている部分の面積と、赤、青、黄色にぬられている部分の面積をそれぞれ求めなさい。
（2）全ての立体の赤くぬられている部分の面積の合計と、青くぬられている部分の面積の合計と、黄色くぬられている部分の面積の合計がどれも同じとき、全ての立体の白くぬられている部分の面積の合計は最も少なくて何cm2ですか。
（3）全ての立体の白くぬられている部分の面積の合計が5652cm2であるとき、立体1、2、3はそれぞれ何個ずつありますか。考えられる個数の組を全て答えなさい。ただし、立体1、2、3はどれも異なる個数あるとします。

【解説と解答】
（１）
立体１　白い部分　25×6×3.14＝150×3.14＝471cm2　赤い部分　6×6×3.14＝113.04
立体２　白い部分　3×2×3.14×20＝376.8cm2　青い部分　3×3×3.14×2＝56.52
立体３　白い部分　4×2×3.14×15＋2×2×3.14×15＝12×3.14×15＝565.2　黄色い部分　（4×4×3.14-2×2×3.14）×2＝75.36cm2
（２）赤：青：白＝36：18；24＝6：3：4なので、同じ面積であれば個数の比は2：4：3になります。
したがって2個、4個、3個だから（150×2＋120×4＋180×3）×3.14＝4144.8
（答え）4144.8cm2
（３）5652÷3.14＝1800　立体1は150、立体２は120、立体３は180ですから、それが合わせて1800になるように決めていきます。
まず計算を簡単にするために、30で割ってしまうと5、4、6で60を作ると考えることになります。
4、6が偶数で、60も偶数ですから立体1は偶数でなければならないので、
以下のような表になります。

受験で子どもと普通に幸せになる方法、本日の記事は
問題を絞って集中する

5年生の教室から
写真を見せる

中学受験　算数オンライン塾
3月28日の問題

にほんブログ村

本来中学受験は小学校で習ったことを前提に試験を作れば良いわけですが、しかし、それだと差が付かない。

それで「小学生でも解けること」という割と曖昧な基準で出題されています。例えば中学で習うことでも、問題文で若干内容を教えた上で答えさせる、というようなスタイルもあり得る。結果として出題範囲はどんどん肥大化していきます。

なので、それを全部やろう、と考えても終わらない。また実際に受験直前期で全部できる必要もない。

ただ志願する学校の問題ができればいいだけの話です。

しかも何校合格しても入学する学校は1校しかない。なので、まずは第一志望校で何が出ているのかをしっかり研究することです。

その上でそれらの問題を解けるために、どんな勉強をしていくかを考えていく必要があります。これまではカリキュラムを勉強しているわけですが、そのすべてが出題されるというわけではありません。

出題されないところを勉強するほど時間的余裕があるわけではないのです。だから、受験準備は志望校に合わせてシンプルに考えていきましょう。

受験で子どもと普通に幸せになる方法、本日の記事は
成功体験がある子

6年生の教室から
上を向く

今日の慶應義塾進学情報
過去問の勉強を始める

にほんブログ村

カリキュラムを前倒しにし、生徒の成績管理をしっかりして、課題を与え、大学受験に向けての準備を着々と進める、というのが管理型の学校です。

ところが良く考えてみると、これはこれまで子どもたちがやってきた受験勉強とあまり変わりがない。

「また、これ？」

みたいな感じになりやすい部分もあるのです。

笛吹けど踊らず、ということになりかねない。かえってその圧迫感がいやでせっかく入った学校をやめてしまう、という場合もあります。

で、学校側も当然気が付いている。本人が勉強をやらないと結局伸ばすことはできない。

だからクラブ活動を推奨したり、将来の道筋を考える機会を与えたり、と多面的に働きかけるようになってきました。

学校に管理してもらえるなら大丈夫、と思いがちですが、本当は「動機がしっかりした上で、自分でがんばろうと思うようになる」ことさえできればいいので、子どもの資質に合わせた学校選びを考えていきましょう。

受験で子どもと普通に幸せになる方法、本日の記事は
メリハリ

5年生の教室から
ごまかさない

中学受験　算数オンライン塾
3月26日の問題

にほんブログ村