2015年聖光学院の問題です。
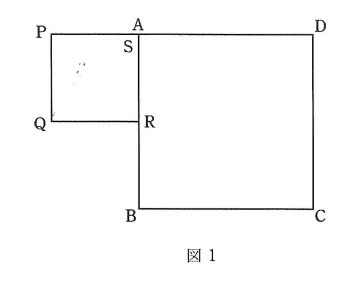
図1のように、1辺の長さが6cmの正方形ABCI)と1辺の長さが3cmの正方形PQRSが、点Sと点Aが重なっていて、辺AB上に点Rがあるように置かれています。図1の状態から、図2のように正方形PQRSが正方形ABCDの周りをすべらないように反時計回りに回転するとき、次の問いに答えなさい。ただし、円周率は3.14とします。
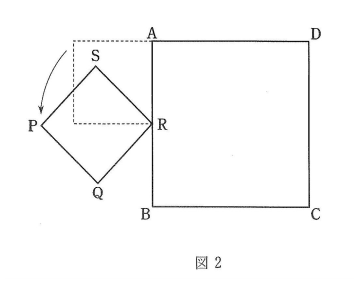
(1) 点Qが点Bに重なるまで正方形PQRSが回転するとき、対角線PRが通過する部分の面積を求めなさい。
(2) 点Qが点Bに重なるまで正方形PQRSが回転するとき、対角線QSが通過する部分を鯨巻線の図に斜線で示し、その部分の面積を求めなさい。
(3) 正方形PQRSが正方形ABCDの周りを回転し、元の図1の状態に戻ってくるとき、対角線QSが通過する部分の面積を求めなさい。
【解説と解答】
(1)
以下のように動きますから、対角線PRが動くのは斜線部分になります。
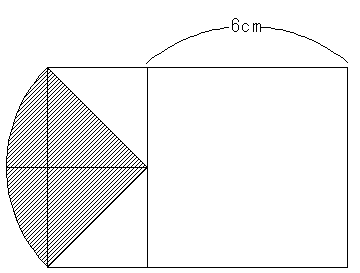
この半径は求められませんが、半径×半径は3×3×2=18になるので、18×3.14×$$\frac{1}{4}$$=14.13cm2
(答え)14.13cm2
(2)以下のように動きます。
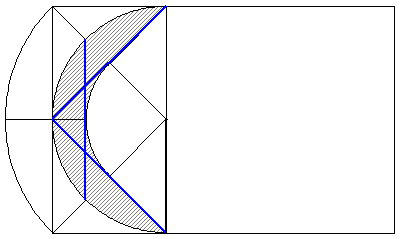
斜線部分の面積は半径3cmの2分の1円から、4.5×3.14×$$\frac{1}{4}$$と3×3×$$\frac{1}{2}$$を引くので
4.5×3.14-1.125×3.14-4.5=10.5975-4.5=6.0975
(答え)6.0975cm2
(3)
もう90°回転すると図のように動きますから、求める面積は
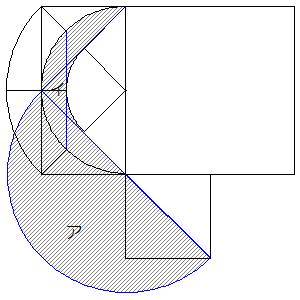
ア4つとイ4つの合計になります。
ア=3×3×2×3.14÷2=28.26より28.26×4=113.04
イ=3×3÷2-4.5×3.14÷4=4.5-3.5325=0.9675 0.9675×4=3.87
よって113.04+3.87=116.91cm2
(答え)116.91㎝2
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
計画は常に修正する
==============================================================
今日の慶應義塾進学情報
普通、得意ではない
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

