2014年早稲田大学高等学院中学部の問題です。
図の四角形ABCDは面積が24cm2の平行四辺形です。辺AD上に点Eを、辺AB上に点F、辺CD上に点Gをとります。さらに3点、H、E、Fと3点、H、B、Cがそれぞれ一直線上になるように点Hをとります。
AF=FB、AE=ED=BH、CG:GD=3:2のとき、色のついた部分の面積を求めなさい。
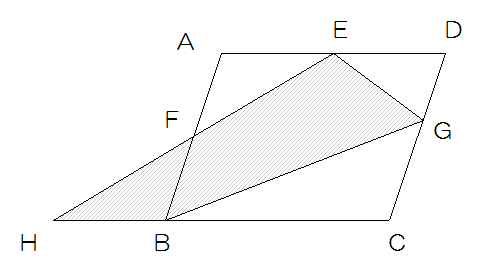
【解説と解答】
三角形AFEと三角形FBHは合同ですから、斜線部分の面積は平行四辺形ABCDから三角形EGDと三角形BCGの面積を引けば良いことになります。
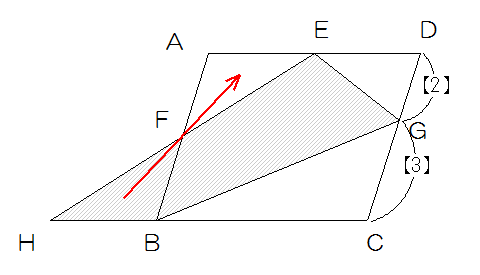
三角形EDGは平行四辺形ABCDの半分の面積である三角形ACDの$$\frac{1}{2}$$×$$\frac{2}{5}$$=$$\frac{1}{5}$$
三角形BCGは平行四辺形ABCDの半分の面積である三角形BCDの$$\frac{3}{5}$$
したがって残された部分は1-$$\frac{1}{2}$$×$$\frac{1}{5}$$-$$\frac{1}{2}$$×$$\frac{3}{5}$$=$$\frac{3}{5}$$
24×$$\frac{3}{5}$$=14.4
(答え)14.4cm2
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
この文章は何を言いたいのか?
==============================================================
今日の慶應義塾進学情報
慶應中等部学校説明会
==============================================================

==============================================================
==============================================================

==============================================================
![]()

