四天王寺中学の問題です。
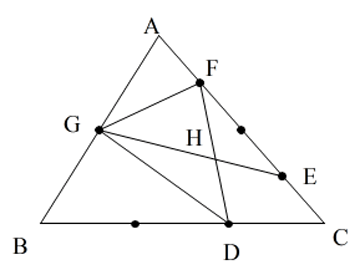
下の図の三角形ABCにおいて、辺BCを3等分する点のうち点Cに近い点をDとし、辺CAを4等分する点のうちもっとも点Cに近い点をE、もっとも点Aに近い点をFとし、辺ABを2等分する点をGとします。また、直線DFと直線EGの交わる点をHとします。
(1)三角形FGDの面積は三角形ABCの面積の何倍ですか。
(2)GH:HEを求めなさい。
(1)
1-![]() ×
×![]() –
–![]() ×
×![]() –
–![]() ×
×![]() =1-
=1-![]() =
=![]()
(答え)![]() 倍
倍
(2)
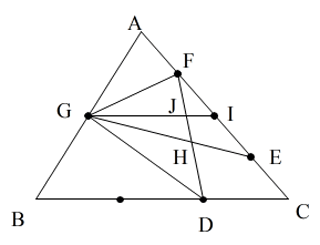
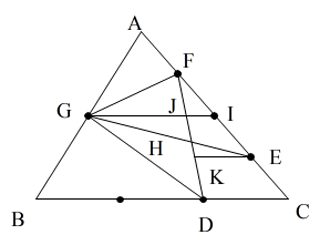
GからACの中点Iに線を引き、FDとの交点をJとします。
DC=12とすると、JI=4 BC=36 GI=18 GJ=14
またEからBCに平行に線を引き、FDとの交点をKとすると、KE=8
よってGH:HE=GJ:KE=14:8=7:4
(答え)7:4
(おことわり)
現在、GOOはメインテナンスを行っておりますので、6月14日の原稿はメインテナンス終了後にアップします。
============================================================
受験で子どもと普通に幸せになる方法、本日の記事は
おかしいことは多いが
==============================================================
今日の慶應義塾進学情報
「自分でやる」への切り替え
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村