2014年東邦大東邦の問題です。
図のようなAD=14㎝の長方形ABCDがあります。
点Pは、点Bを出発して辺BA上を毎秒1cmの速さで点Aまで動きます。
点Qは、点Pが出発してから3秒後に点Dを出発して、辺DA上を毎秒2cmの速さで点Aまで動きます。点Pと点Qが同時に点Aに着くとき、次の問いに答えなさい。
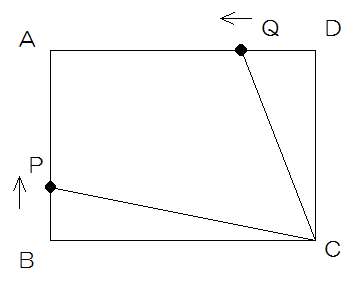
(1)辺ABの長さを求めなさい。
(2)四角形APCQの面積が長方形ABCDの面積の半分になるのは、点Pが点Bを出発してから何秒後ですか。
【解説と解答】
(1)点Pと点Qは同時に点Aに着きます。
ADは14㎝で点Qは秒速が2cmですから、AD上を移動するのにかかる時間は14÷2=7秒。点Qは点Pが出発してから3秒後に出るので、点PはBからAまで7+3=10秒かかります。したがってAB間は1×10=10㎝
(答え)10㎝
(2)四角形APCQの面積は長方形ABCDの面積から三角形PBCと三角形CDQの面積を引いたものですから、四角形APCQが長方形ABCDの半分になるということは、2つの三角形の面積の和が長方形ABCDの半分になります。
点Qが出発してからの時間を【1】秒後とすると
三角形PBCの面積は(【1】+3)×14÷2=【7】+21
三角形QDCの面積は2×【1】×10÷2=【10】
したがって合計は【17】+21=10×14÷2=70
より(70-21)÷17=$$\frac{49}{17}$$=2$$\frac{15}{17}$$
したがって点Pが出発してからは3+2$$\frac{15}{17}$$=5$$\frac{15}{17}$$秒後です。
(答え)5$$\frac{15}{17}$$秒後
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
危ない考え方
==============================================================
今日の慶應義塾進学情報
志望順位
==============================================================

==============================================================
==============================================================

==============================================================
![]()

