2017年明大明治の問題です。
川の上流にある北町と下流にある南町との間18kmを往復し続ける2種類の船A,Bがあります。Aは各町に到着してから次に出発するまですべて同じ休けい時間をとり,Bも各町に到着してから次に出発するまでAと同じ休けい時間をとります。上りと下りにかかる時間の比は,Aが6:5,Bが5:4です。午前9時にAは北町を,Bは南町を同時に出発すると,午後0時42分にAは南町に到着し,Bは南町を出発します。川の流れの速さは毎時3km、静水時の船の速さはA,Bそれぞれ一定とするとき,次の各問いに答えなさい。
(1)AとBが最初にすれちがうのは出発してから何分後ですか。
(2)到着してから次に出発するまでの休けい時間は何分間ですか。
(3)AとBが3回目にすれちがうのは午前何時何分ですか。
流速は、下りと上りの速さの差の半分になるので、Aの下りの速さは時速36km、上りは30km。Bは下りの速さが時速30km、上りの速さが24kmとなります。
したがって北町と南町の間は18kmあるので、Aは下りに30分、上りに36分、Bは下りに36分、上りに45分かかることになります。
Aは一往復に66分かかります。9時から12時42分までの間は222分で、最後に南に着くので、2往復+1片道だと66×2+30=162分 4回休憩するので1回の休憩時間は15分と考えられます。3往復+1片道だと、66×3+30=228分で条件に合わず、1回往復だと96分になるので、2回休憩するから、1回の休憩が65分になります。
一方Bは1往復に81分かかります。午後0時42分に出発するので、2往復+4回の休憩時間は=222分 222-81×2=60 60÷4=15分となり、これがあてはまります。
Bが1往復だとする場合、222-81=141分 141÷2=70.5分となり、休憩時間がAと同じにはなりません。
(1)最初にすれ違うのは、18÷(36+24)×60=18分後
(答え)18分後
(2)
(答え)15分
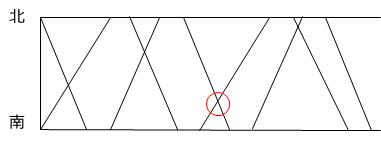
(3)グラフよりBが2度目に出発した後、3回目にすれ違います。
1往復後の出発時刻は9時+81+15×2=10時51分。一方、Aは1往復して2度目に出発しているので、66分+15分×2=96分ですから10時36分に出発しているので、15分経っているから、半分のところまで来ています。9÷(36+24)×60=9分後ですから、10時51分+9分=11時に3回目にすれ違います。
(答え)11時
受験で子どもと普通に幸せになる方法、本日の記事は
受験勉強に終わりはない
5年生の教室から
解法を覚える
今日の慶應義塾進学情報
学校別単科特別コース 若干名募集のお知らせ