2016年 海城中学の問題です。
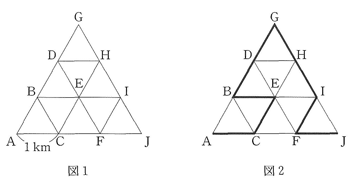
図1のように、AからJまでの10個の地点があり、各地点が長さ1kmの道でつながっています。A地点を出発し、道に沿ってJ地点まで行くルートを考えます。
ただし、一度通った地点は再び通れないものとします。
(1)道のりが4kmのルートは何通りありますか。
(2)道のりが9kmのルートが全部で何通りあるかを、AからEまで行くのに何km進むかによって分けて考えます。次の[ア]、[イ]、[ウ]にあてはまる数を答えなさい。
AからEまで2kmで、EからJまで7kmであるルートは図2の1通りです。
AからEまで3kmで、EからJで6kmであるルートは[ア]通りです。
AからEまで4kmで、EからJまで5kmであるルートは[イ]通りです。
このように考えていくと、道のりが9kmのルートは全部で[ウ]通りあります。
【解説と解答】
(1)AJの間で1kmが3本あるので、その上のB、E、Iのどれかを通る方法が3通り。ABEIJが1通り。BEとEIを通る方法が2通り。合計6通り。
(答え)6通り
(2)Eまで3kmで行く方法はABDE、ABCE、ACBE、ACFEの4通り。ABDEを選ぶと、残り6kmの道はありません。
ABCEを選ぶと、EDGHIFJとなり、ACBEもEDGHIFJとなり、ACFEはEBDGHIJとなるので3通り。
Eまで4kmはABCFEとなり、EDGHIJの1通り。
Eまで5kmはABDGHEでEGFIJの1通り。
Eまで6kmはABDGHIEで、残りECFJがあるので1通り。ACBDGHEで、残りEIFJとEFIJがあるので2通り。
Eまで7kmはACBDGHIEで残り、EFJで1通り。
合計10通りです。
(答え)ア 3 イ 1 ウ 10
受験で子どもと普通に幸せになる方法、本日の記事は
子どものすることだから
5年生の教室から
成功体験が自信を生む
今日の慶應義塾進学情報
付属校人気の裏側