2015年筑波大駒場の問題です。
辺BCの長さが20cmで、辺ADと辺BCが平行である台形ABCDがあります。
図1のように、辺BC上に2点P、Qがあり、直線APと直線DQが交わる点をRとします。
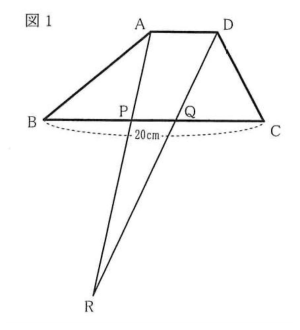
また、BP、QCの長さをともに8cmとすると、三角形ABPと三角形PQRの面積が等しくなります。
次の問いに答えなさい。
なお、4点B、P、Q、Cはこの順にならんでいて、PQの長さはADの長さより短いものとします。
(l)辺ADの長さは何cmですか。
(2)図2と図3の台形ABCDは、図1の台形ABCDと同じ台形です。
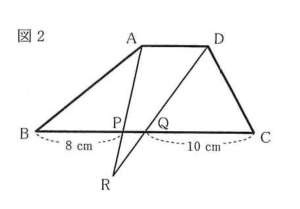
(ア)図2のように、BPの長さを8cm、QCの長さを10cmにしました。三角形PQRの面積は、(1)のときの面積の何倍になりますか。
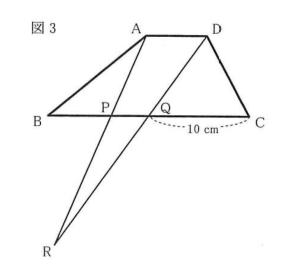
(イ)図3のように、QCの長さを10cmにして、BPの長さをある長さにしたとき、三角形ABPと三角形PQRの面積が等しくなりました。このとき、BPの長さは何cmですか。
【解説と解答】
(1)BP=8cm QC=8cmのときPQ=4cm 底辺の比が2:1ですから、三角形ABPと三角形PQRの面積が2倍になるためには、AP:PR=1:2になるので、AD=4÷2×3=6cmになります。
(答え)6cm
(2)
(ア)PQ=2cmですから、AP:PR=2:1です。
底辺が半分になり、高さは4分の1ですから、面積は8分の1です。
(答え)8分の1
(イ)
三角形ABPと三角形PQRの面積が等しいので、台形ABQDと三角形ARDの面積が等しいことになります。
台形の面積を【26】とすると、三角形QDCはQC=10cmより【10】
したがって、【16】が三角形ARDの面積になるから、ADは6cmより高さは、
16÷6=$$\frac{8}{3}$$倍になるので、
AP:PR=3:5
よって、BP:PQ=5:3
10÷(5+3)×5=6.25cmになります。
(答え)6.25cm
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
覚える技術
==============================================================
今日の慶應義塾進学情報
普通部ばかり?
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

