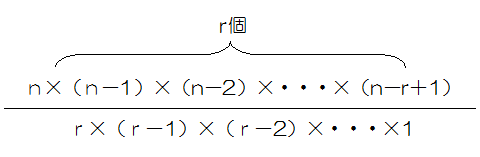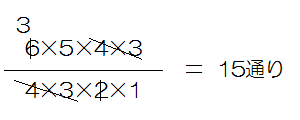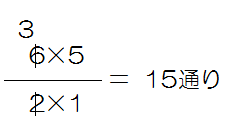今週は速さのいろいろな文章題を考えていきましょう。

---

（例題１）
行きは分速120ｍ、帰りは分速80ｍでした。平均の速さは分速何ｍですか。

---

（解説と解答）
割と間違いやすい問題でしょう。
速さを平均するというと（120＋80）÷2＝100ｍと考えがちですが、そうではありません。

例えば1200ｍの距離を行きは分速120ｍで行くと1200÷120＝10分
帰りは1200ｍ÷80＝15分　合計10＋15＝25分で合計1200×2＝2400ｍ移動するのだから速さは2400÷25＝96ｍになるのです。

往復の速さは往復の距離を、全体にかかった時間で割ることで計算します。

（答え）96m

---

（例題２）
太郎君は家から毎分120ｍで駅に向かいました。途中、公園で休憩し、その後は分速80ｍで駅に向かいました、グラフは出発してからの時間と家からの距離を表しています。

グラフのアとイにあてはまる数を答えなさい。

---

（解説と解答）
図のようなグラフをダイヤグラムと言います。最初の速さは分速120ｍなので120×８＝960ｍ進んでいますからアは960ｍです。
家から公園まで960ｍでした。その後２分休んでいます。グラフが上下に動いていないので、そこで止まっていることがわかります。
その後分速80ｍになりました。家から駅までの距離はグラフから2000ｍとわかるので、公園から駅までは
2000－960＝1040ｍになります。
したがって1040÷80＝13分、公園から駅までかかるのでイは10＋13＝23分になります。
（答え）ア　960　イ　23
このように進んでいく様子をグラフに表して、その中に情報が組み込まれている場合もあるので、グラフの読み方をしっかり覚えてください。

---

（例題３）
太郎君は家から2000ｍ離れた駅まで分速120ｍで向かいました。しかし、途中で分速が80ｍになったので、結局家から駅まで24分かかりました。
速さを変えたのは家から何ｍのところですか。

---

（解説と解答）
これは速さのつるかめ算です。
分速80ｍで24分行くと80×24＝1920ｍしか行けません。2000－1920＝80ｍ不足します。
したがって分速80ｍを分速120ｍに変えていくことを考えます。120－80＝40ｍですから、1分変えると40ｍ増えます。
80÷40＝2分ですから、120ｍで歩いたのは2分間だったことがわかります。
速さを変えたのは120×2＝240ｍです。
確かめてみましょう。
2000－240＝1760ｍ　1760÷80＝22分ですから2分＋22分＝24分で2000ｍ行くことができます。
（答え）240ｍ

---

（例題４）
太郎君は分速120ｍで4分歩いては1分休みます。次の問いに答えなさい。

（１）太郎君は家から駅まで22分かかりました。家から駅までは何ｍですか。
（２）太郎君は駅からさらに1200ｍ離れた図書館に歩いて向かいます。駅から図書館まで何分かかりますか。

---

（解説と解答）
（１）5分で1セットと考えます。このとき太郎君は120×4＝480ｍ進むので、
22÷5＝4…2より4セットありますから480×4＝1920ｍ　残りの2分は分速120ｍですから1920＋120×2＝2160ｍが家から駅までの距離になります。
（答え）2160ｍ

（２）1200ｍ÷120＝10分歩かなければなりません。10÷4＝2･･･2より休憩は2回です。
したがって10＋1×2＝12分
（答え）12分

基本的な問題を並べてみましたが、入試の問題はさらに発展していきます。グラフも単に移動している様子だけではなく、二人の間の距離を表す問題などもあります。難しい問題も少しずつ考えていきながら、条件を把握する力や応用力を身に付けていきましょう。

以下のプリントもお役立ていただければと思います。

算数オンライン塾　速さ（２）

==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は

志望校が決まりません！
==============================================================
今日の慶應義塾進学情報

過去1年間の成績を調べてみると
==============================================================

==============================================================
お知らせ
算数５年前期第19回　算数オンライン塾「旅人算とグラフ（２）」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

にほんブログ村

今週は素因数分解について説明しましょう。

素数というのは、１とその数以外に約数を持たない整数のことをいいます。１は素数ではありません。１から10までの整数の中で素数は２、３、５、７の４つになります。

整数を考えるとき、その整数をいくつかの素数の積に分解することを素因数分解といいます。小学生はまだ累乗は勉強しませんから、ただ横に並べて書くだけですが、例えば24という整数は
２×２×２×３と分解することができます。つまり、24は２が３つと３が１つ掛け合わされてできた整数だと言えるのです。この素因数分解を使って、いろいろな入試問題が作られていますが、まず基本的なところからご紹介しましょう。

（例題１）
200という整数には何個の約数がありますか。

（解説と解答）
約数が何個あるか、は素因数分解を使って解くことができます。
200を素因数分解すると2×2×2×5×5になります。200の約数はこのどれかをつかってできています。例えば4は200の約数ですが2×2と2を2つ使ってできているのです。素因数分解すると2は3つ、5は2つありますから、2の使い方は「使わない」という場合を含めて4通りの使い方があります。一方5は2個ありますから、「使わない」という場合を含めて3通りの使い方があります。したがって約数は4×3＝12個になるのです。2も5も使わないのが1になります。

では正しいか確かめてみましょう。200の約数を1から小さい順に書き出してみましょう。

1、2、4、5、8、10、20、25、40、50、100、200と12個になりました。

このようなやり方で約数の個数を求めることができます。
（答え）12個

（例題２）
２つの整数AとBがあります、AとBの最大公約数は24、AとBの最小公倍数は144です。AがBよりも大きい時、Aはいくつですか。

（解説と解答）
AとBの最大公約数が24ですから、A＝24×a B＝24×bと置くことができます。　このときaとｂには公約数が1以外にはありません。もし1以外の公約数があれば、24は最大公約数にはならないからです。
このようにお互いに1以外に約数がない関係のことを「互いに素」といいます。

AとBの最小公倍数が144ですから144＝24×a×bと置くことができるので、a×b＝6　になります。a＞bですから（a,b)＝（6,1)か（3,2)になります。したがってAは24×6＝144か24×3＝72になります。

（答え）144、72

（例題３）
1×2×3×･･･×100の積を3で繰り返し割っていきます。何回割り切ることができますか。

（解説と解答）
1×2×3×･･･×100を素因数分解したとき、3が何個でてくるか？という問題です。その個数分だけ3で割り切れることになります。

1～100までに3の倍数は100÷3＝33･･･1より33個あります。3×3=9ですから、最初の3は数えていますが、うしろの3は数えていません。1～100までに9の倍数は100÷9＝11･･･1ですからあと11個増えます。

3×3×3＝27で最初の2つは3の倍数、9の倍数で数えましたが、最後の3は数えていません。100÷27＝3･･･19よりあと3個増えます。

最後に3×3×3×3＝81があります。100÷81＝1･･･19であと1個増えるので、合計は33+11+3+1＝48個あるので、48回割り切れることになります。

（答え）48個

（例題４）
1×2×3×･･･×40までの積は1の位から何個0が続きますか。

（解説と解答）
この問題は良く入試で見かける問題でしょう。1の位に0がつくというのは10倍された、ということです。10を素因数分解すると2×5=10ですから1×2×3×･･･×40を素因数分解したときに5が何個あるかを調べれば良いことになります。（2の数は5の数より多いので、5の数の分だけ1の位から0が続くのです。）

40÷5＝8　5×5＝25ですから、最初の5は数えていますが、後ろの5は数えていませんので40÷25＝1･･･15より全部で8+１＝9個あるので9個0が続きます。

（答え）9個

（例題５）
1から50までの整数が書かれている50枚のカードがあります。裏には何も書かれていません。1番から50番までのゼッケンをつけた生徒50人がいます。1番の生徒はすべてのカードを裏返しました。数字が表になっているカードは1枚もありません。次に2番の生徒が2の倍数のカードをすべて表にします。次に3番の生徒が3の倍数のカードを裏になっているのは、表に、表になっているのは裏に、していきます。同様に4番の生徒は4の倍数、5番の生徒は5の倍数、とずっと続けていき、最後に50番の生徒まで同じ作業をしました。作業が終わったとき、カードが裏になっている番号をすべて答えなさい。

（解説と解答）
1番が全部裏返した後、1は誰も作業をしないので裏のままです。2番が2の倍数を表にします。その後2は一度も触られないので、2は表のままです。3は3番が表にした後、一度も作業されないので表のままです。4は2番が表にした後、今度は4番が裏にします。その後はだれも作業をしないので、4は最後まで裏です。

この違いを考えると、約数の個数であることに気が付きます。2は約数が1と2、3は約数が1と3と偶数個あるので、カードは表になります。しかし、4は約数が1、2、4と奇数個あるので、裏になるのです。

したがって1から50までに約数が奇数個ある数は何かを考えれば良いことになります。4が奇数個になった理由は2×2＝4であったからです。つまり同じ数を2回かけてできる整数は約数が奇数個になるのです。

その整数は2×2＝4、3×3＝9、4×4＝16、5×5＝25　6×6＝36　7×7=49と1が裏でおわります。

（答え）1、4、9、16、25、36、49

最近は数の性質の問題が増えてきて、素因数分解が使われることが多くなりました。平方根は中学校の範囲の問題ですが、答えが整数であればA×A＝324も素因数分解でAを求めることができます。

324＝2×2×3×3×3×3＝18×18と組み立てることができるのでAは18だとわかるのです。

したがって素因数分解を柔軟に使えるようにしておくことが大切です。

以下のプリントもお役立ていただければと思います。

算数オンライン塾　数の性質

==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は

ギリギリよりは余裕のある合格の方が良いか？
==============================================================
今日の慶應義塾進学情報

湘南台からの時間
==============================================================

==============================================================
お知らせ
算数５年前期第19回　算数オンライン塾「旅人算とグラフ（２）」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

にほんブログ村

今週は場合の数の組み合わせについて考えます。

組み合わせは、順列の考え方を応用して計算します。すなわち順列を計算して、１つの組み合わせをいくつの順列としているか計算して割るのです。

例えばABCDの４人の中から３人を選ぶ組み合わせは、順列で考えると

4×3×2＝24通りになります。

で、ABCという組み合わせは3×2×1＝6通りで計算しているので、

24÷6＝4通り　となるわけです。4人の中から3人を選ぶ場合、残る1人の選び方は4通りですから、答えは4通りとわかりますが、組み合わせの公式はこのようにしてできています。

n個の中からr個を選ぶ組み合わせの公式は、

となっていますが、分子がｎ個の中からr個を選ぶ順列、分母が１つの組み合わせを何通りに順列に計算しているか、になっているわけです。

（例題１）
ABCDEFの6人がいます。これについて次の問いに答えなさい。
（１）4人の掃除当番を決める決め方は何通りありますか。
（２）2人の日直を決める決め方は何通りありますか。

（解説と解答）
（１）6人の中から4人を選ぶのですから、

になります。

（２）同様に6人の中から2人を選ぶのですから、

になります。

答えが同じになるのは偶然ではなく、これが同じ問題であるからです。4人の掃除当番を決めるということは、掃除当番でない2人を決めることと同じです。つまり6人の中から4人を決める組み合わせは6人の中から2人を決める組み合わせと同じことになるのです。

（例題２）
正十二角形の対角線の数を求めなさい。

（解説と解答）
それぞれの分野で公式がありますが、組み合わせの考え方から生まれた公式もあります。
正十二角形には12個の点があります。その1つの点からは自分と両隣を引いた9個（12－3＝9）の点に対して対角線を引くことができます。ただしAからBとBからAは同じ対角線ですから1つの対角線を2本で計算することになるので、
12×（12－3）÷2＝54本になります。

（例題３）
オリンピックのサッカーでは16か国が参加します。16か国を4つのグループに分けて総当たり戦を行います。その結果、上位2チームが決勝トーナメントを行い、1位から3位までを決めます。3位決定戦を含めて試合数は全部で何試合ありますか。

（解説と解答）
1つのグループは16÷4＝4か国ですから、組み合わせは4×3÷2＝6試合あります。したがって4つのグループでの試合数は6×4＝24試合。
上位2チームが決まって4グループで決勝トーナメントに参加する国は2×4＝8か国。トーナメントは勝ち抜き戦ですから、1試合で必ず1チームが負けます。金メダルのチームだけが負けないので、決勝トーナメントの試合数は8－1＝7試合。
これに3位決定戦が1試合加わるので合計8試合。
したがって試合数は全部で24＋8＝32試合になります。
（答え）32試合

（例題４）
以下の図の中に四角形は何通りありますか。

（解説と解答）
1つの四角形はたての線2本、横の線2本で決まります。たての線は4本あるので、組み合わせは4×3÷2＝6通り　横の線は3本あるので、組み合わせは3×2÷2＝3通りですから、四角形は全部で
6×3＝18個あります。

別の考え方で検証してみましょう。
1つの正方形でできている四角形は6個。
2つの正方形を横に並べてできる四角形は4個
2つの正方形をたてに並べてできる四角形は3個
3つの正方形を横に並べてできる四角形は2個
4つの正方形を並べてできる四角形は2個
6つの正方形を並べてできる四角形は1個
ですから、合計6＋4＋3＋2＋2＋1＝18個
になります。

（答え）18個

（例題５）
なしが3個、みかんが2個、りんごが2個あります。この中から3つを選んでジュースをつくります。ジュースのつくり方は何通りありますか。

（解説と解答）
これはやや面倒な問題です。
なし3個の中では区別がつきませんから、単純に公式を使うわけにはいきません。

なし、なし、なし、
なし、なし、みかん、なし、なし、りんご
なし、みかん、みかん、なし、みかん、りんご、なし、りんご、りんご、
みかん、みかん、りんご、　みかん、りんご、りんご

となるわけですが、ここで気を付けなければいけないのは、同じ組み合わせを排除するルールを作っておくことです。

一番上はなしが3個、2番目はなしが2個、3番目はなしが1個、4番目はなしを使わない場合で分けています。
またなしを最初にかき、つぎにみかんを書き、りんごを最後に書くので、りんごの右になしやみかんが出てこないようにします。

こうすることで重複をせずに書き出すことができるでしょう。
（答え）8通り

組み合わせはこのように、公式だけでできる問題ばかりではありません。場合を分けたり、条件を整理して書き出すなどの作業が必要になる問題の方がむしろ多いので、重複を許さないような書き方を工夫していかなければなりません。書き出すこともいとわず、むしろ整理してきちんと作業できるようにしっかり練習していきましょう。

以下のプリントもお役立ていただければと思います。

算数オンライン塾　場合の数　組み合わせ

==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は

馴染める学校を選ぶ
==============================================================
中学受験　算数オンライン塾

5月26日の問題
==============================================================

==============================================================
お知らせ
算数５年前期第18回　算数オンライン塾「旅人算とグラフ（１）」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

にほんブログ村