割合を学習するとき、こんな問題が良く例題になります。
ある商品を仕入れ、仕入れ値の3割増しの定価をつけました。そして定価の２割引きで売ったところ、１つについて160円の利益がありました。この商品の仕入れ値はいくらですか。
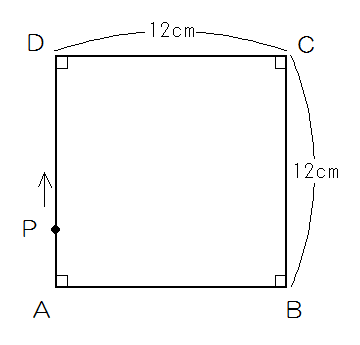
まずは、線分図をかいて、ことばの説明をします。
3割の利益というのは、もとを仕入れ値にしている。したがって仕入れ値が10割に対して、利益は3割だから定価は仕入れ値の13割にあたります。
で、ここから2割引くという時は、もとにする量が定価に変っている。だから2割引く、つまり0.8倍するのは仕入れ値の13割に対して0.8倍することになるから1.3×0.8＝1.04で仕入れ値の４％が160円にあたる、ということを説明するわけです。
慣れてくると、子どもたちも仕入れ値を1として
1×1.3×0.8－1＝0.04＝160円 160÷0.04＝4000円
というような式を書いて行けるわけですが、問題はもう少し面倒になって、例えばこんな問題になったとき。
太郎君は持っているお金の$$\frac{1}{3}$$よりも200円少ないお金で本を買い、残りの$$\frac{3}{5}$$よりも100円多いお金でノートを買ったら、最初のお金の$$\frac{1}{4}$$が残りました。太郎君は最初いくらもっていましたか。
$$\frac{1}{3}$$より200円少ないお金を使えば、$$\frac{2}{3}$$より200円多いお金が残り、$$\frac{3}{5}$$よりも100円多いお金を使えば$$\frac{2}{5}$$よりも100円少ないお金が残るので、
（$$\frac{2}{3}$$＋200）×$$\frac{2}{5}$$－100＝$$\frac{1}{4}$$
でこのとき、割合のかけ算と、お金のかけ算がいっしょになるので、それを区別するように考えた智慧ものがいたわけです。
で、割合には○を付けた。
こうすると、最初のお金が①であることがよくわかる。これがマルイチ算の由来です。
私は、WEB上では【1】にしています。まあ、これはWEBだから仕方がない部分がありますが。
したがって式は
（【$$\frac{2}{3}$$】＋200）×$$\frac{2}{5}$$－100＝【$$\frac{1}{4}$$】
【$$\frac{4}{15}$$】＋80－100＝【$$\frac{1}{4}$$】
【$$\frac{16}{60}$$】＋80－100＝【$$\frac{15}{60}$$】
【$$\frac{1}{60}$$】＝20円
【1】＝1200円
ということになるわけです。
で、これを見たとき、だれもが何だ、一次方程式じゃないか、と思われるでしょう。
だから、じゃあ、方程式を教えればいいんじゃないの？ということになりそうですが、実はこれは単に割合の部分を明確にしているにすぎません。
１にするか①にするか、だけの話。それでミスを減らそうとしているのです。で○がついたから、特別にマルイチ算とどこかの塾か、教材会社が別のテーマとして切り分けましたが、結局は割合の文章題に過ぎないのです。
だから、この解き方を見て、一次方程式を教える方法は、かえって子どもたちにいろいろな負担を強いることになる、と思ってください。
例えば移項を教えるということは、正負の数を考えなければいけなくなる。等号の左側と右側が同じだから、同じ数を足しても、引いても等号関係は変わらないから、と言われて、子どもたちはもっと困惑するのです。
マルイチ算は単に割合に区別をつけるだけの話ですから、「じゃあ、一次方程式」とは置き換えず、単に割合を区別するということだけを確認してあげてください。
============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
中学受験はしないが、先先は心配だから、という場合の塾選び
==============================================================
今日の慶應義塾進学情報
基本を大事に
==============================================================
==============================================================
==============================================================
にほんブログ村
図１
図1－1
図1－2
図1－3
図2－1
図2－2
図3－1
図4－1
図5－1
図6－1
図6－2
図6－3
