旅人算とグラフの2回目です。円周上を回る旅人算や往復の旅人算について考えていきましょう。
(例題1)
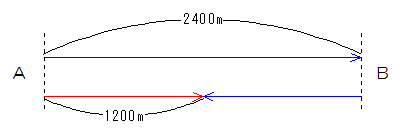
周りの長さが1200mの池の周りをA君とB君が同時に出発します。ふたりが同じ方向に向かうと20分後にA君がB君を追い抜き、反対の方向に行くと4分後に出会うそうです。
A君とB君の分速を求めなさい。
(解説と解答)
同じ方向に行けば、二人の速さの差で広がっていきちょうど1周分の差がついたときにA君がB君を追い越します。
1200÷20=60mが二人の分速の差。
反対の方向に行けば、二人の速さの和で間が縮まっていくので、ちょうど1周分縮まれば二人が出会います。
1200÷4=300mが二人の分速の和。
あとは和差算なので(60+300)÷2=180mがAの分速。300-180=120mがBの分速になります。
(答え)A 180m B 120m
(例題2)
1周1800mの池の周りをA、B、Cの3人が同じ地点から同時に、同じ方向に向かって歩き始めます。Aの分速は100m Cの分速は180mです。
(1)CがAを始めて追い抜くのは出発して何分後ですか。
(2)CはAに追いついてから6分後にBに追いつきました。Bの分速は何mですか。
(解説と解答)
(1)二人の差は180-100=60mですから1800÷20=30分後
(2)CがBに追いついたのは36分後になります。このときCは180×36=6480m動いていますが、Bよりも1周多く動いているのでBが動いた距離は6480-1800=4680m
これを36分で動くのだから4680÷36=130m
(答え)130m
(例題3)
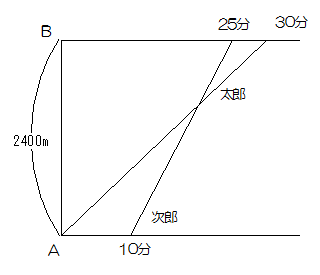
AB間は2400m離れています。今Aから太郎君と次郎君が同時に出発してAB間の往復を繰り返します。
太郎君が最初に次郎君と出会ったのは出発して20分後でした。次の問いに答えなさい。
(1)二人が2回目に出会うのは何分ですか。
(2)太郎君が3往復したとき、二郎君は2往復して同時にAにもどりました。太郎君の分速を求めなさい。
二人の動きをグラフにすると以下のようになります。
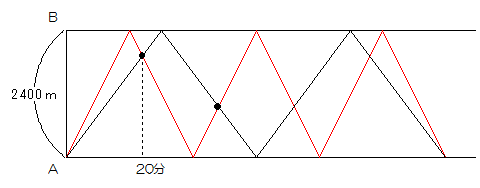
(1)二人は1回目に出会うまでに合わせて2400×2=4800m動いでいることがわかります。それにかかる時間が20分です。
次に2回目に出会うときは二人で合わせて2400×4=9600m移動していますから2倍の時間がかかります。したがって20分×2=40分です。
(答え)40分
(2)太郎君が3往復するのに次郎君が2往復ですから、太郎君は次郎君の1.5倍の速さになります。
二人の分速の和は4800÷20=240mですから、240÷(1+1.5)=96mが二郎君の速さになるので、太郎君の速さは
240-96=144mです。
(答え)144m
(例題4)
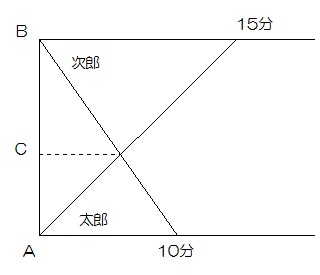
AからBまで1200mあります。Aから太郎君がBから次郎君が同時に向かい合って出発しました。二人は出発してから15分後に出会い、その後AB間の往復を繰り返しました。次の問いに答えなさい。
(1)二人が2回目に出会うのは出発して何分後ですか。
(2)太郎君が次郎君にAで初めて追いつきました。それぞれの分速を求めなさい。
二人の動きをグラフにすると次のようになります。
今度は向かい合っていますので、最初に出会うのは二人で合わせて1200m動いたときです。
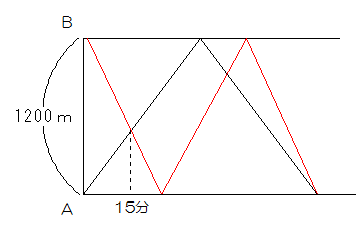
2回目に出会うのは、二人で合わせて1200×3=3600m歩いたときですから、
3600÷1200=3より15×3=45分
(答え)45分
(2)グラフから太郎君が二郎君に追いつくのは二人で合わせて1200×5=6000m動いたときですから、15分×5=75分かかります。このとき太郎君は1200×3=3600m動いているので
3600÷75=48mが太郎君の分速になり、次郎君は1200×2=2400m動いているので2400÷75=32m
(答え)太郎君 48m 次郎君 32m
(例題5)
A君とB君がPから、C君がQから同時に向かい合って出発し3人ともPQ間の往復を繰り返します。
PQ間は2400mでA君の分速は80m、B君の分速は120m、C君の分速は40mです。次の問いに答えなさい。
(1)A君とB君が初めて出会うのはPから何mのところですか。
(2)B君とC君が初めて出会う場所からA君とC君が初めて出会う場所までの間の距離は何mですか。
(1)A君とB君が初めて出会うのは二人で2400×2=4800m移動するときですから、
4800÷(80+120)=24分後 したがってPからは80×24=1920mになります。
(答え)1920m
(2)B君とC君が初めて出会うのは2400÷(120+40)=15分後
A君とC君が初めて出会うのは2400÷(80+40)=20分後
したがってその間にC君は5分移動するので、間の距離は40×5=200m
(答え)200m
速さの問題は条件がいろいろ出てくるので、まずそれを正確に読み取ることが大事です。条件がグラフで出されることもあれば、文章で出されることもありますが、グラフを使うとどういう動きになるのか視覚化できるので、考えるべきポイントを絞りやすくなります。
グラフを上手に使えるように練習してください。
以下のプリントもお役立ていただければと思います。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
時間がかかるなら、かければいい
==============================================================
中学受験 算数オンライン塾
7月7日の問題
==============================================================

==============================================================
夏休みの学習にお役立てください、

==============================================================

==============================================================
![]()
にほんブログ村