今回は三角形の相似を発展させて、いろいろな図形の面積を求める問題と影の問題を考えます。
(例題1)
図のような長方形ABCDがあり、EはADの中点、FはDC上の点でDF:FC=1:3です。
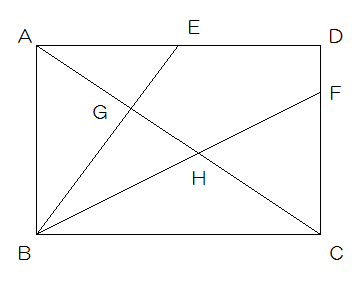
次の問いに答えなさい。
(1)BH:HFを求めなさい。
(2)AG:GH:HCを求めなさい。
(解説と解答)
(1)三角形ABHと三角形HFCは相似です。AB:FC=1+3:3=4:3になるので、
BH:HF=4:3になります。
(答え)4:3
(2)(1)からAH:HC=4:3
また三角形AGEと三角形GBCの相似から、AG:GC=1:2
4+3=7 1+2=3より7と3の最小公倍数21をACとすると、
AG=21÷3=7 HC=21÷(4+3)×3=9より、GH=21-7-9=5
したがってAG:GH:HC=7:5:9
(答え)7:5:9
(例題2)
図のような台形ABCDがあり、角DAE、角EBCはそれぞれ直角です。
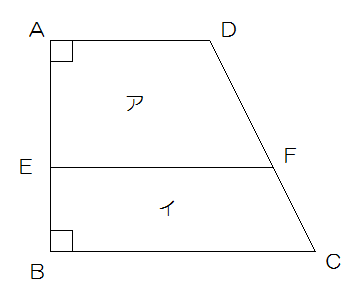
EはAB上の点、FはDC上の点で、ADとEFは平行。DF:FC=3:2
AD=6cm、BC=10㎝ です。次の問いに答えなさい。
(1)EFの長さを求めなさい。
(2)台形アと台形イの面積の比を求めなさい。
(1)図のようにDからBCに垂線を下ろし、BCとの交点をH、EFとの交点をGとします。
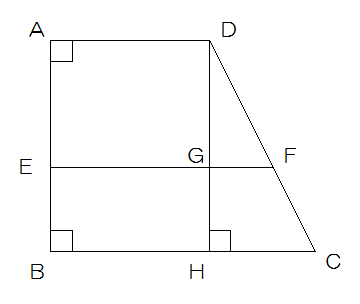
AD=EG=BH=6cm HC=10-6=4cm
三角形DGFと三角形DHCの相似からHC:GF=3+2:3=5:3より
GF=4×$$\frac{3}{5}$$=2.4cm
よってEFの長さは6+2.4=8.4cm
(答え)8.4cm
(2)アの上底+下底は6+8.4=14.4 イの上底+下底=8.4+10=18.4
14.4:18.4=72:92=18:23
高さの比は3:2になるので、18×3:23×2=54:46=27:23
(答え)27:23
(例題3)
図のように直角三角形ABCと長方形BDECを組み合わせました。ADとBCの交点をF、ADとBEの交点をGとします。
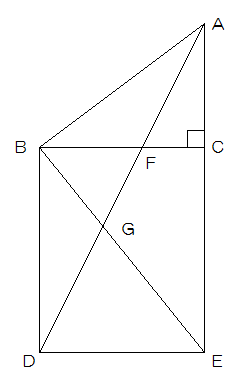
三角形ABFの面積が15㎝2、三角形AFCの面積が9cm2になりました。次の問いに答えなさい。
(1)BG:GEを求めなさい。
(2)四角形FGECの面積を求めなさい。
(解説)
(1)三角形ABFと三角形AFCは高さがACと共通ですから、BF:FC=15:9=5:3
三角形AGFと三角形GDEは相似で、BF:DE=5:5+3=5:8ですから、BG:GE=5:8です。
(答え)5:8
(2)三角形AFCと三角形ADEの相似からAC:AE=FC:DE=3:8
よってAC:CE=3:8-3=3:5 三角形ABC=15+9=24㎝2より、三角形BCE=24÷3×5=40cm2
BF:FC=5:3、BG:GE=5:8より
四角形FGEC=40×(1-$$\frac{5}{8}$$×$$\frac{5}{13}$$)=40×$$\frac{104-25}{104}$$
=40×$$\frac{79}{104}$$=$$\frac{395}{13}$$=30$$\frac{5}{13}$$
(答え)30$$\frac{5}{13}$$cm2
(例題4)
長さが1mの棒の影が1.8mでした。図のような木の影が10.8m離れた壁に高さ2mまで来ていた時、この木の高さは何mですか。
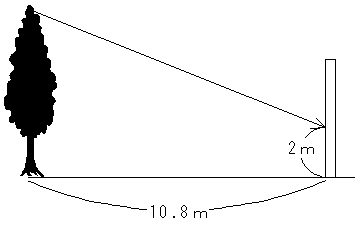
(解説)
1mの棒の影が1.8mですから1:1.8=5:9です。
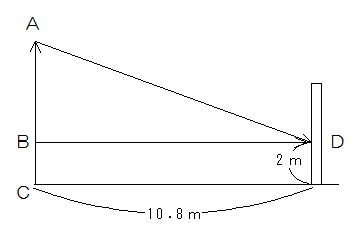
AB:BD=5:9ですからAB=10.8÷9×5=6m
BC=2mですから木の高さは6+2=8mです。
(答え)8m
(例題5)
6mの街灯があり、そこから7.2mのところに太郎君が立っています。太郎君の身長は1.5mです。次の問いに答えなさい。
(1)このときの太郎君の影の長さは何mですか。
(2)太郎君が今立っているところから、街灯から離れるように毎秒2mで進みます。太郎君の影の長さが、12mになったのは出発してから何秒後ですか。
(解説)
(1)
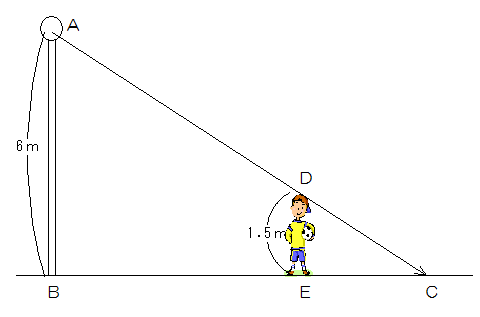
街灯の高さと太郎君の身長は決まっています。
したがって三角形ABCと三角形DECの比は常に6:1.5=4:1になるので、BE:EC=3:1になります。
BE=7.2mのとき、EC=7.2÷3=2.4mですから、太郎君の影は2.4mです。
(答え)2.4m
(2)太郎君の影の長さが12mですから、太郎君は街灯から12m×3=36m離れたことになります。36-7.2=28.8mより
28.8÷2=14.4秒
(答え)14.4秒後
三角形の相似を使って、いろいろな図形の面積を求める問題は、単に平面だけではなく立体にも応用できます。したがって、この範囲は良く出題されますから、しっかり得意にしてください。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
ここからは強気
==============================================================
今日の慶應義塾進学情報
再修制度
==============================================================

==============================================================
お知らせ
算数5年後期9回 算数オンライン塾「規則性に関する問題」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村







