今週は流水算について説明していきたいと思います。流水算は川を下ったり上ったりするときに、川の流れの速さによって速さが変わる問題です。いろいろ条件を付けやすい分、最近の入試問題では良く出題されているテーマです。ここではしっかりとまず基本を身に付けていきましょう。
1 流れの速さと静水時の速さ
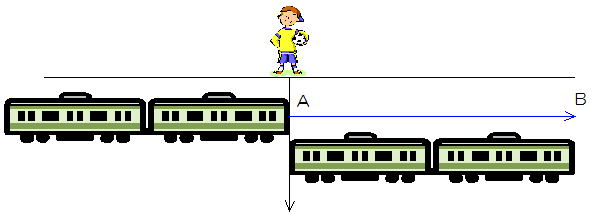
流水算ではこの2つの速さが問題に出てきます。流れの速さというのは、川の水の速さのことです。例えば上流のA地点からいかだを流すと、このいかだは下流に向かって流れていきます。このいかだの速さは流れの速さと同じになります。
一方静水時の速さというのは、流れがないとことで船が移動する速さのことです。流水算では、この2つの速さで下りの速さと上りの速さが計算できます。
2 下りの速さと上りの速さ
下りの速さは、静水時の速さ+流れの速さです。流れに沿って下るので、川の速さが船の速さに加わることになります。
上りの速さは、静水時の速さ-流れの速さです。流れに沿って上ると、川の速さで流される分、船の速さは静水時の速さより遅くなることになります。
ここで、式をよく見ると、下りの速さと上りの速さの差は流れの速さの2倍になっていることがわかります。
これを線分図で見ると、

というようになります。
したがって、こんな公式が生まれることになります。
(下りの速さ-上りの速さ)÷2=流れの速さ
で、逆に静水時の速さを出す場合は、
(下りの速さ+上りの速さ)÷2=静水時の速さ
という式を使えばいいことがわかります。これは和差算と同じですね。
この公式は覚えておくと、いろいろな場面で使えるので、覚えておくと良いでしょう。流水算は速さの問題ですから、比を利用して解くことができます。これまで速さと比について学習してきたので、それも踏まえながら例題を学習していきましょう。
(例題1)
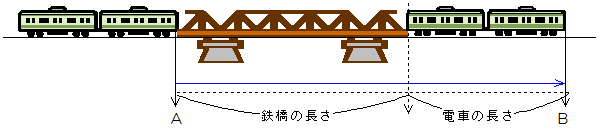
上流のAから下流のBまで2400mあります。流れの速さは分速50mです。静水時の分速が200mの船がBからAまで上るとき、かかる時間は何分ですか。
(解説と解答)
求めるのは上りにかかる時間ですから、上りの速さを出します。
上りの速さは静水時の速さ-流れの速さでした。
したがってこの場合は200-50=150mになります。
かかる時間は2400÷150=16分になります。
(答え)16分
(例題2)
上流のAから下流のBに向かって4時間、BからAへ6時間かかる船があります。流速は分速40mです。この船の静水時の時速は何kmですか。
(解説と解答)
この問題のカギは、同じ距離を動く時間が提示されていることです。
下りは4時間、上りは6時間ですから、かかる時間の比は2:3。ということは下りの速さ:上りの速さ=3:2という比が出ます。
そうすると、先ほどの公式に当てはめることができます。すなわち、下りの速さを【3】、上りの速さを【2】とすると
(【3】-【2】)÷2=【0.5】=分速40mということになるので、 【1】=40÷0.5=80m
下りの速さは80×3=240m・・・分速ということになります。
流れの分速が40mですから、静水時の分速は240-40=200mになるので、時速は200×60÷1000=12kmになります。
(答え)時速12km
(例題3)
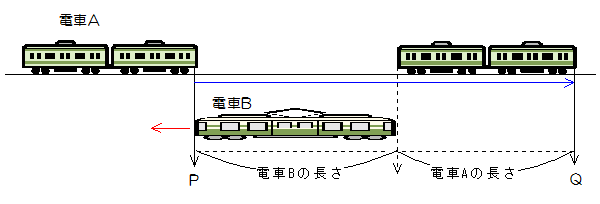
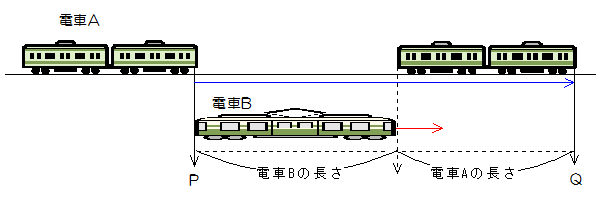
上流のAから下流のBに向かってP船が、BからAに向かってQ船が同時に出発しました。P船は出発して4時間後にQ船とすれちがい、その後2時間でBに到着しました。P船とQ船の静水時の速さは同じです。
またこの川の流れの速さは分速60mでした。このとき次の問いに答えなさい。
(1)Q船はBからAまで何時間かかりましたか。
(2)AからBまで何mですか。
(解説と解答)
(1)これも良くでる形です。グラフで考えると、以下のようになります。

2つの船がすれ違った場所をCとすると、BC間をP船は2時間で通過しているのに対して、Q船は4時間かかっていることになるので、かかる時間の比は1:2です。
したがってQ船は(4+2)×2=12時間かかります。
(答え)12時間
(2)同じ距離を移動するのにかかる時間の比が1:2ですから、P船の下りの速さ:Q船の上りの速さ=2:1になります。
2つの船の静水時の速さは同じですから、差の半分が分速60mになるので(【2】-【1】)÷2=【0.5】=60m 【1】=60÷0.5=120mですから、P船の下りの分速は120×2=240mです。
分速240mは時速240×60÷1000=14.4kmですから、14.4×6=86.4kmがAB間の距離になります。
(答え)86.4km
(例題4)
Aさんは長さ60mの動く歩道に乗って、その上を歩ききるのに20秒かかります。ある日、この動く歩道が故障して止まっているとき、Aさんはこの動く歩道の上を歩ききるのに48秒かかりました。Aさんがこの動く歩道に乗って歩かないとすると何秒かかりますか。
(解説と解答)
流水算は川の流れ以外にも動く歩道やエスカレータ-の問題にも応用できます。
60mを20秒かかって行くとき、歩道の速さ+Aさんの速さ=60÷20=3mの秒速になります。
一方、Aさんが歩く速さは60÷48=$$\frac{60}{48}$$=$$\frac{5}{4}$$=1.25mになります。
したがって動く歩道の速さは3-1.25=1.75mになります。
60÷1.75=60÷$$\frac{7}{4}$$=$$\frac{240}{7}$$=34$$\frac{2}{7}$$
(答え)34$$\frac{2}{7}$$秒
(例題5)
川の上流のA地点から下流のB地点まで太郎君は船に乗って出発する1時間前に、ボールを川に流しました。そして船で出発して30分後にそのボールに追いつき、その後1時間で太郎君はB地点に着きました。太郎君の船の静水時の速さは分速80mです。
次の問いに答えなさい。
(1)ボールは太郎君がBに到着してから何時間後にBに到着しますか。
(2)川の流れの速さは分速何mですか。
(解説と解答)
(1)太郎君がボールに追いつくまで、A地点から30分ですが、ボールはそこまで1時間30分かかっています。
したがって太郎君は1時間30分でBに到着しましたから、ボールは1時間30分×3=4時間30分かかります。
ボールがB地点に到着するのは、太郎君がBに到着してから4時間30分-1時間30分-1時間=2時間後です。
(答え)2時間後
(2)下りの速さ:川の流れの速さ=3:1より、その差の2が静水時の速さです。80÷2=40m
(答え)40m
流水算の基本について解説しました。入試問題に出題される流水算はここのところ、かなり複雑になっていますが、基本は以上のポイントになります。速さと時間の関係、上りなのか、下りなのかなど、条件を確認しながら解き進んでいきましょう。
以下の教材もお役立てください。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
問題を先に見ておこう
==============================================================
今日の慶應義塾進学情報
本人が志望理由を書く
==============================================================
お知らせ
算数5年後期12回 算数オンライン塾「流水算」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村