7月に入りました。

まもなく夏休みが始まります。夏休みは受験前、自由な時間が長くとれる機会ではあるものの、実際には夏期講習があってなかなか自分の勉強ができない、というところもあるかもしれません。

これまでの勉強のデータが集まっているので、ここを復習したい、とか、ここを練習したいという気持ちがあるでしょうが、なかなか全部はやりきれません。ですから、「絶対にやりあげるもの」を決めましょう。決めるといっても、具体的に時間があるか、調べてみないと決められません。（気合いだけではだめです。）

塾の講習時間や、復習や宿題にかかる時間を差し引いて、いったいあと、どのくらい勉強する時間があるのか、計算してみましょう。加えて過去問も宿題になる可能性があるでしょうから、やはり、相等少なくなる、と考えないといけないのです。

あれもやりたい、これもやりたいはなかなか難しいので、「これは絶対」というものに絞り込んでいきましょう。

============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は

海外の大学への進学実績
============================================================
中学受験　算数オンライン塾

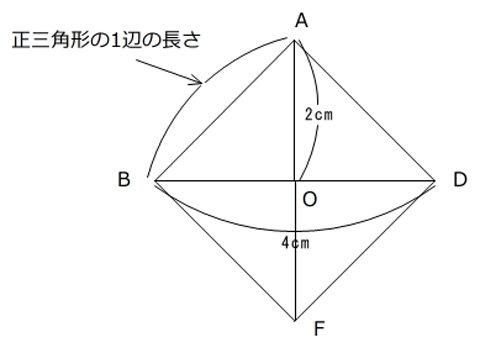
7月1日の問題
==============================================================

==============================================================

==============================================================

==============================================================

にほんブログ村

0620

最近の中学受験の準備を見ていると、「楽に力がつくわけがない」という前提ではないか、と思われるがごとくにハードです。

まだ11才とか12才の子が、夜遅くまでやっても、体力が続かないし、またあまり残らない、というようなことは考えない。日々気合いを入れて努力する、みたいな姿が求められているのかもしれませんが、体力のある中学生や高校生の受験ではありません。

したがってむしろ「どうやったら楽に力がつくか」というのを考えていかなければいけない。

楽にやるためには絞るしかないのです。絞るということは、「出題される問題」に絞る必要がある。出ない問題に絞ったらまたまた効果がありません。したがって自分が受ける学校に出る問題は何か？ということを考えて、勉強を進めるのが一番良い。

だからといって、ヤマをかけるのはないのです。過去出題された問題をしっかり分析して出題傾向を探り、そのレベルの問題に特化していく。土台、あれもこれもとできるわけはないのだから、「楽にやる方法」を見つけるのが一番正しい。

今やっている勉強が、「楽な方法」かどうかは、やはりしっかり吟味をしていく必要があるでしょう。

============================================================
受験で子どもと普通に幸せになる方法、本日の記事は

算数で解き方を書かせる学校の狙い
==============================================================
今日の慶應義塾進学情報

場合の数の問題
==============================================================

==============================================================

==============================================================

==============================================================

にほんブログ村

2016年東邦大東邦の問題です。

図のような．大きさの等しい正三角形を八つ合わせてできる立体ABCDEFがあります。BDの長さは4cmです。頂点Bに、この立体の1辺と等しい長さのひもの先端をつけました。　このとき、次の問いに答えなさい。
（1）この立体の体積を求めなさい。
（2）この立体の表面上で、ひものもう一方の先端Pが届く範囲の面積を求めなさい。
ただし、円周率は3.14とし、答えは小数第3位を四捨五入して小数第2位まで求めなさい。

【解説と解答】
(1)図のように、四角形ABFDは正方形になります。

したがってBDとCEの交点をOとすると、OA＝2cm。また四角形BCEDも正方形になるので、その面積は4×4÷2＝8cm2ですから、この立体の体積は8×2×2×$$\frac{1}{3}$$＝10$$\frac{2}{3}$$

（答え）10$$\frac{2}{3}$$cm3

(2)
動く範囲は正三角形の1辺を半径とした中心角60°×4のおうぎ形になります。
正三角形の1辺の長さはわかりませんが、1辺の長さ×1辺の長さ＝4×4÷2＝8
したがって8×3.14×$$\frac{1}{6}$$×4＝$$\frac{10048}{600}$$≒16.746…
から16.75cm2
（答え）16.75cm2

「映像教材、これでわかる比と図形」（田中貴）

============================================================
受験で子どもと普通に幸せになる方法、本日の記事は

しつこく考える
==============================================================
今日の慶應義塾進学情報

制服
==============================================================

==============================================================

==============================================================

==============================================================

にほんブログ村