桜蔭中学の問題です。
つぎの文章を読み、下の問いに答えなさい。
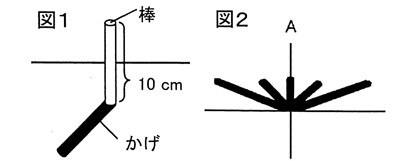
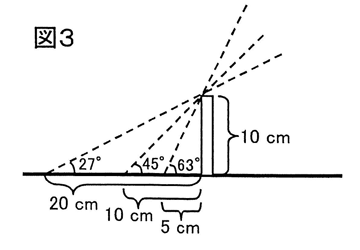
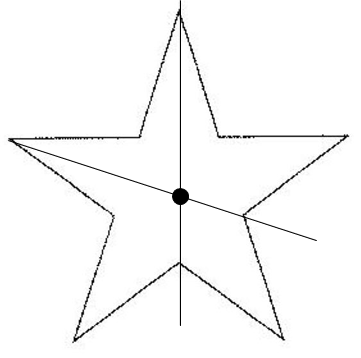
春分の日、関東のある地点(北線35度、東経140度)において、図1のように、長さ10cmの棒を地面に垂直に立て、一定時間ごとにかげを調べたところ、図2のようになりました。
問1 図2のAの方位を答えなさい。
問2 かげが最も短くなるのはいつですか。つぎのア~ウから1つ選び、記号で答えなさい。
ア.12時より前 イ.12時 ウ.12時より後
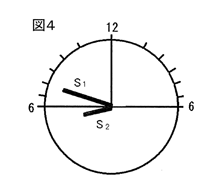
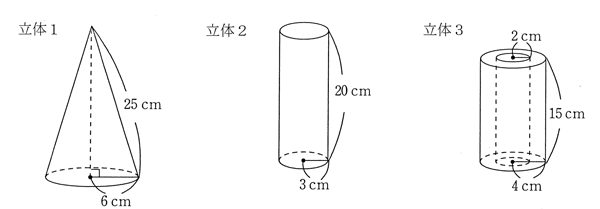
問3 かげが最も短くなる時のかげの長さはどうなりますか。図3を参考にして、つぎのア~エから1つ選び、記号で答えなさい。
ア.5cmより短い イ.5cm以上10cm未滴 ウ.10cm以上20cm未満 エ.20cm以上
春分の日のかげのようすをもとにして、午前6時から午後6時までの1時間ごとに目盛りを刻んだ日時計を作りました。
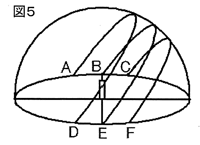
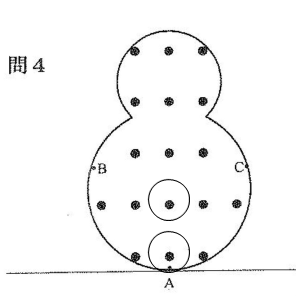
図4はそのばん面で、春分の日のある時刻のかげS1が書かれています。ところが、別の日の同じ時刻におけるかげは、S2のようになり、異なる向きになってしまいました。
問4 S1のかげができた時刻は、春分の日のア.午前8時、イ.午後4時 のどちらですか。記号で答えなさい。
問5 S2のかげができたのはどの日ですか。つぎのア~ウから1つ選び、記号で答えなさい。
ア.夏至 イ.秋分 ウ.冬至
問6 つぎの文章中の①~⑤に適するものを、それぞれ選び、記号で答えなさい。
図5は、春分、夏至、冬至の太陽の通り道を、とうめい半球(太陽などの天体がその球面を移動しているように見立てたもの)上に表したものです。この図5のA~Fのうち、夏至の日の入りの位置は、(①)になります。図5から、棒を垂直に立てたとき、季節によって、同じ時刻のかげの向きが異なることがわかります。
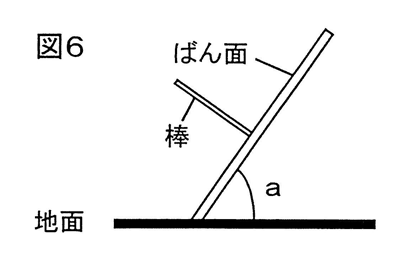
そこで、図6のように、棒の向きが地軸(北極と南極を結んだ軸)と平行になるようにばん面をかたむけました。
これにより、かげができているときは、異なる季節であっても、同じ時刻のかげの向きが同じになります。このとき、棒の先たんの向きは(②ア.東 イ.西 ウ.南 エ.北)、ばん面と地面との角度aは(③ア.35 イ.23.4 ケ55 ェ.66.6)です。
また、ばん面をかたむけたことで、太陽の通り道がつくる面とばん面が平行になります。
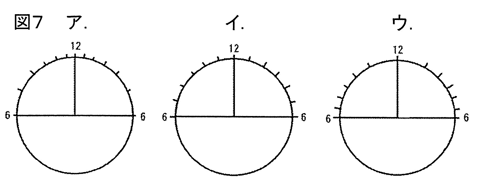
そのため目盛りの間かくは図7のア~ウのうち、(④)になります。そして、7月1日の午後3時のかげの長さは、同じ日の正午のかげの長さと比べると、(⑤ア.短く イ.同じに ウ.長く)なります。
【解説と解答】
問1 影は北側に出ます。(答え)北
問2 正午に南中するのは明石です。この東経では12時より前に南中します。(答え)ア
問3 春分の日の南中高度は90-緯度です。したがって55°。45°で10cmですから、それより短く、63°のときよりは長くなるからイになります。(答え)イ
問4 西側に影ができていますから、太陽は東側にいるので、午前中です。(答え)ア
問5 影が東西の線を切っていますので、夏至です。(答え) ア
問6 夏至はAーDですが、日の入りですからD。棒の先端は北、緯度と同じ角度で傾けます。傾けたことで、間隔は等しくなり、影の長さは等しくなります。
(答え)①D ②エ ③ウ ④イ ⑤イ
受験で子どもと普通に幸せになる方法、本日の記事は
幼さとの戦い
5年生の教室から
親が焦らない
中学受験 算数オンライン塾
4月1日の問題