音に関する問題 | 中学受験　田中貴.com

2021年海城中学の問題です。

次の文を読み、以下の各問いに答えなさい0数値で答えるものは、必要であれば四捨五入して整数で答えなさい。

　　物が振動すると、まわりの空気が振動します。その振動が空気中を伝わり、私たちの耳の鼓膜を振動させると、私たちはそれを音として感じることができます。私たちのまわりには様々な音がありますが、昔の違いは、昔の三要素とよばれるもので区別できます。
　問1　音の三要素とは何ですか。それぞれ答えなさい。

　図1は、鍵盤の一部です。①の鍵盤と②の鍵盤は、どちらも弾くと「ド」の音が出ますが、②は①より1オクターブ高い「ド」、逆に言うと、①は②より1オクターブ低い「ド」になります。この違いは、振動数の違いで生じています。振動数は、音を発しているものが1秒間に何回振動しているかを表しており、単位はHz（ヘルツ）を用います。②の振動数は①の振動数の2倍になっています。また、例えば①と③のように、白い鍵盤と黒い鍵盤の区別なく、となり合う鍵盤の振動数は、右側が左側の1.06倍になっています。

　
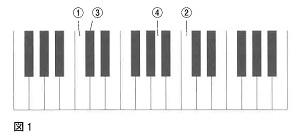
　問2　④の鍵盤を弾くと振動数が440Hzの「ラ」の音が出ます。②の鍵盤を弾いたときに出る音の振動数は何Hzですか。必要であれば、
1.06×1.06＝1.12

1.06×1.06×1.06＝1.19

1.06×1.06×1.06×1.06＝1.26

1.06×1.06×1.06×1.06×1.06＝1.34

1.06×1.06×1.06×1.06×1.06×1.06＝1.42

　として計算しなさい。

問3　①の鍵盤を弾いたときに出る音の振動数は何Hzですか。

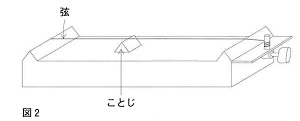
　図2のようなモノコードとよばれる装置は、弦を張る強さを変えたり振動させる弦の長さを変えたりはじき方を変えたりすることで、出る音を変えることができます。

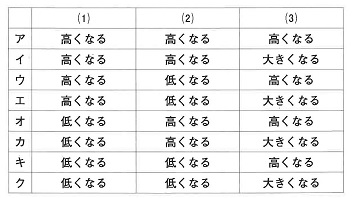
問4　モノコードでの音の出し方を、次の（1）~（3）のように変えてみます。そのときの音は、変える前の音と比べて、それぞれどのように変わりますか。下のア～クから適当な組み合わせを1つ選び、記号で答えなさい。

（1）弦を強く張る。
（2）ことじを動かして弦の振動する部分の長さを短くする。
（3）弦を強くはじく。

問5　弦を別のものに張りかえても、音を変えることができます。張りかえる弦は同じ材質のものを使うことにします。弦の張る強さと振動する長さは同じままで、高い音を出すには、どのような弦に張りかえればよいですか。

　ギターは、太さの異なる6本の弦を張った楽器（図3の右側が第1弦，左側が第6弦）で、弦を押さえる場所（フレット）を変えながら、弦を弾いて音を出します。ギターのような弦楽器は、演奏に用いる前にチューニングという作業をします。ギターでは、まず第5弦をどこのフレットも押さえずに弾いたときに出る音の振動数が440Hzになるように、弦を張る強さを調整します。次に、第5弦を張る強さは変えないで、第6弦を5フレットを押さえて弾いたときと、第5弦をどこも押さえないで弾いたときの音の振動数が同じになるように、第6弦を張る強さを調整します。同じようにして、以下の
　第5弦を5フレットを押さえたときと、第4弦をどこも押さえないとき
　第4弦を5フレットを押さえたときと、第3弦をどこも押さえないとき
　第3弦を4フレットを押さえたときと、第2弦をどこも押さえないとき
　第2弦を5フレットを押さえたときと、第1弦をどこも押さえないとき

の4組の音がそれぞれ同じ振動数になるように、第4弦～第1弦を張る強さを調整していきます。

問6　チューニングを終えたギターは、第1弦をどこも押さえないで弾いたときに出る音と第6弦をどこも押さえないで弾いたときに出る音はどちらも「ミ」の音になりますが、2オクターブ異なります。高い「ミ」の音が出るのはどちらの弦ですか。

問7　間6の「ミ」の音で、一方の音の振動数は1319Hzです。他方の音の振動数は何Hzですか。

【解説と解答】
問l　音の３要素は強弱、高低、音色です。
（答え）音の強弱・音の高低・音色
問2　鍵盤で３つ違います。したがって440×1.06×1.06×1.06＝440×1.19＝523.6≒524
（答え）524
問3　1オクターブで2倍ですから、524÷2＝262
（答え）262
問4　弦を強く張れば音は高くなります。また弦の振動する部分を短くすれば、これも音は高くなります。強くはじけば音は大きくなります。したがってイ。
（答え）イ
問5　弦を細くすることで音は高くなります。
（答え）細い弦
問6　高い「ミ」の音がでるのは1弦。1弦をおさえないときと2弦で5フレットをおさえた音が同じなのですから、どちらもおさえなければ1弦の方が高い音が出るということです。
（答え）1
問7　2オクターブですから2×2＝4倍になっているので1319÷3＝329.75≒330となります。
（答え）330

今後、投稿のタイミングを定時以外に増やしていきます。投稿のタイミングをTwitterでお知らせしていますので、ぜひフォローしてください。
田中貴のTwitter