天体に関する問題 | 中学受験　田中貴.com

2020年聖光学院の問題です。

次の文章を読んで，あとの（1）～（5）の問いに答えなさい。
　太陽と地球と月の3つの天体について考えます。太陽の直径は約1400000km，地球の直径は約12800km，月の直径は約3500kmなので，太陽の直径は地球の直径の約109倍，月の直径は地球の直径の約0.27倍となります。また，太陽の直径は月の約400個分の長さとなります。

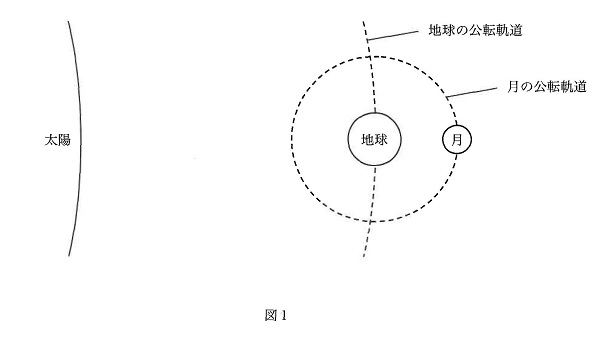
　図1のように，地球は太陽の周りを，そして，月は地球の周りを公転しています。このとき，どちらの公転軌道も円であるとすると，地球の公転軌道の直径は約300000000km，月の公転軌道の直径は約770000kmとなります。また，公転軌道を1周するのにかかる時間を公転周期といいますが，地球の公転周期は約365日，月の公転周期は約27日です。

（1）　月の公転軌道の円周の長さは，月何個分ですか。最も適したものを，次の（ア）～（エ）の中から1つ選び，記号で答えなさい。ただし，円周率は3.14とします。
（ア）　約200個　　　（イ）　約350個　　　（ウ）　約690個　　　（エ）　約1380個
（2）月が1時間で公転する距離は，月何個分ですか。最も適したものを，次の（ア）～（エ）の中から1つ選び，記号で答えなさい。
（ア）　約1個　　　　（イ）　約2個　　　　（ウ）　約25個　　　（エ）　約28個
（3）地球から見たとき，月は1時間で公転軌道を月何個分動いているように見えますか。ただし，答えが割り切れない場合は，小数第1位を四捨五入して整数で答えなさい。
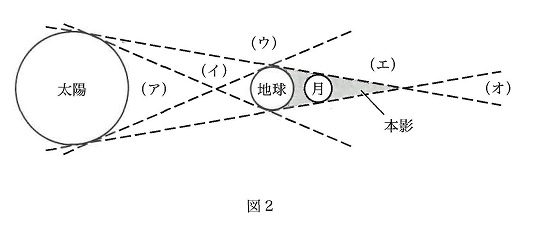
（4）　図2は，地球上で月食が観測されるときの太陽と地球と月の場所の関係を表しています。太陽の光を地球がさえぎると，2種類の暗い場所ができます。最も暗い場所を本影、少し暗い場所を半影といいます。図2の中で，半影はどこですか。（ア）～（オ）の中から1つ選び，記号で答えなさい
。

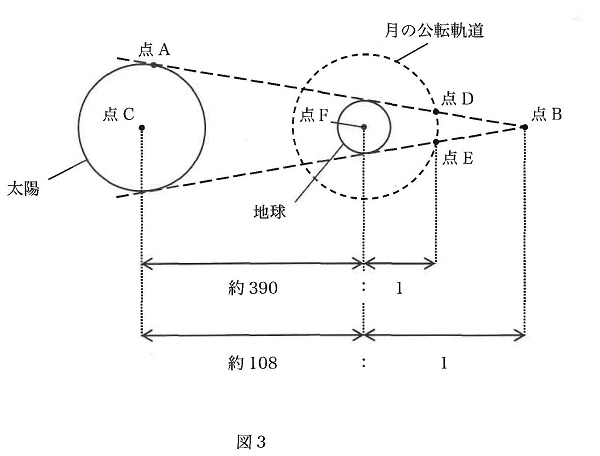
（5）　図3は，太陽と地球と月の大きさや距離の関係を模式的に表したものです。これを使って，本影が月の軌道と重なる部分の長さを計算してみます。次の文章は，その計算方埠の手順を述べたものです。あとの（a）・（b）の問いに答えなさい。ただし，角DBEが小さな値なので，本影が月の軌道と重なる部分DEは円の弧ですが，直線であると考えます。

太陽と地球の距離CFと，地球の中心Fから点Bまでの距離FBの比は，太陽の直径と地球の直径の比から求めることができ，約108：1と表すことができます。地球の公転軌道の半径CFと月の公転軌道の半径の比は約390：1と表すことができます。これら2つの比から，月の公転軌道の半径と地球の中心Fから点Bまでの距離FBの比は1：（あ）となります。

このことから，本影が月の公転軌道と重なる部分DEの長さは，地球の（い）個分の長さとなります。
（a）　（あ）にあてはまる数値として最も適したものを，次の（ア）～（エ）の中から1つ選び，記号で答えなさい。
（ア）　約1.6　　　（イ）　約2.6　　　（ウ）　約3.6　　　（エ）　約4.6
（b）　（い）にあてはまる数値として最も適したものを，次の（ア）～（エ）の中から1つ選び，記号で答えなさい。
（ア）　約0.18　　（イ）　約0.36　　（ウ）　約0.72　　（エ）　約0.92

【解説と解答】
（１）月の公転軌道の直径が77万kmですから公転軌道はその3.14倍で、月の直径は0.35万kmですから、77×3.14÷0.35≒690からウ。
（答え）ウ
（２）月の公転軌道が690個分。24×27＝648時間ですから、およそ1個。
（答え）ア
（３）地球が自転しているので、1時間には360÷24＝15度動いて見えます。1周が690個分なので、690÷24＝28.75　しかし1個分は公転しているので、27.75個分になるから、28個
（答え）28個
（４）半影はエ。
（答え）エ
（５）CFの長さを390×108とすれば390：1＝390×108：108
108：1＝390×108：390から月の公転軌道の半径：FB＝108：390＝１：3.61から（あ）はウ
390－108＝282　390：282＝1：0.72
から（い）もウ。
（答え）a ウ　b　ウ

Newフリーダム進学教室からのお知らせ
冬期講習のお知らせ