2017年開成中学の問題です。
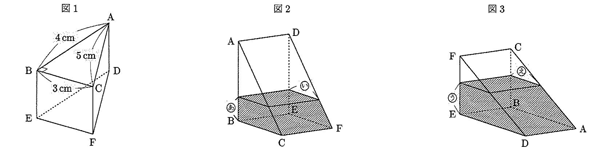
図1のように、底面がAB=4cm、BC=3cm、CA=5cm、角ABCの大きさが90°の三角形であり、側面がすべて長方形の透明な三角柱のガラスでできた容器があります。この容器には水を入れることができ、どのような向きに置いても水はもれないものとします。また、容器のガラスの厚さは考えません。
まず、この容器に少し水を入れたところ、面DEFを下にして水平な床に置いたときと、図2のように面BCFEを下にして水平な床に置いたときとで、容器の下の面から水面までの高さが等しくなりました。
次に、この容器に、これまでに入っていた量の$$\frac{5}{4}$$の水をさらに追加したところ、面DEFを下にして水平な床に置いたときと、図3のように面ABEDを下にして水平な床に置いたときとで、容器の下の面から水面までの高さが等しくなりました。
ただし、下の図において斜線の部分は入っている水を表しています。次の問いに答えなさい。
(1)図3のうの長さは、図2のあの長さの何倍ですか。
(2)図3のえの長さは、図2のいの長さより何cm長いですか、または短いですか。解答らんの「長い」「短い」のいずれかに○印を付け、その差を答えなさい。
(3)図2のあの長さは何cmですか。
(4)BEの長さは何cmですか。
(5)図3の状態のあと、この容器に水をさらに追加したところ、面DEFを下にして水平な床に置いたときと、面ACFDを下にして水平な床に置いたときとで、容器の下の面から水面までの高さが等しくなりました。このとき、等しい水面の高さは何cmですか。
【解説と解答】
(1)$$\frac{5}{4}$$倍の水を入れたら$$\frac{9}{4}$$になるので、底面積は$$\frac{9}{4}$$です。
三角形DEFを底面としたとき、それぞれ同じ高さになっているので、(あ)と(う)の長さの比は4:9になっているから、2$$\frac{1}{4}$$倍です。
(答え)2$$\frac{1}{4}$$倍
(2)
図2でCFを高さとしたときの底面積:図3でCFを高さとしたときの底面積の比も4:9から
両方の台形の上底+下底は等しくなります。(高さである(あ):(う)=4:9)
下底が図3の方が1cm長いので、上底は図3の方が1cm短くなります。
(答え)(え)の方が1cm短い。
(3)
(あ)の長さを【4】とすると、(う)の長さは【9】になります。
したがって(い)の長さは(4-【4】)÷4×3=3-【3】
(う)の長さは(3-【9】)÷3×4=4-【12】
したがって3-【3】+3=4+4-【12】
【9】=2より【1】=$$\frac{2}{9}$$
(あ)の長さは$$\frac{2}{9}$$×4=$$\frac{8}{9}$$
(答え)$$\frac{8}{9}$$cm
(4)(い)の長さは$$\frac{7}{3}$$cm
したがって容積は($$\frac{7}{3}$$+3)×$$\frac{8}{9}$$÷2×BE=3×4÷2×$$\frac{8}{9}$$
($$\frac{7}{3}$$+3)×BE=12 BE=2$$\frac{1}{4}$$
(答え)2$$\frac{1}{4}$$cm
(5)求める高さを【1】とすると、体積は【6】 一方面ACFDを底面としたときの上底の長さをAとすると
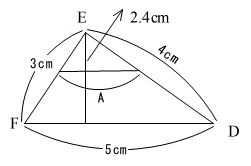
(A+5)×【1】÷2×$$\frac{9}{4}$$=【6】となるので
(A+5)=6×2÷$$\frac{9}{4}$$=$$\frac{16}{3}$$ A=$$\frac{1}{3}$$
したがって水の入っていない部分の高さは$$\frac{1}{3}$$×$$\frac{3}{5}$$×$$\frac{4}{5}$$=$$\frac{4}{25}$$=0.16から2.4-0.16=2.24cm
(答え)2.24cm
受験で子どもと普通に幸せになる方法、本日の記事は
チェックリスト
5年生の教室から
解答の清書
今日の慶應義塾進学情報
傾斜配点