2016年桐朋中学の問題です。
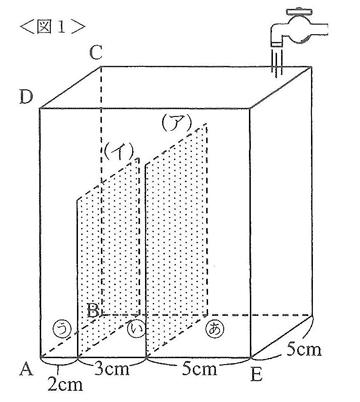
<図1>のような直方体の形をした空の水そうが水平な床の上においてあります。この水そうは面ABCDに平行な2枚の長方形の仕切り(ア)、(イ)によって3つの部分 あ、い、うに分けられています。
仕切り(イ)の高さは仕切り(ア)の高さよりも低くなっています。この水そうのあの部分に水を毎分24cm3の割合で12分30秒間入れました。このとき水はあの部分にいっぱいにたまってから、仕切り(ア)をこえてあふれ、いの部分に5cmの高さまでたまりました。
(1)仕切り(ア)の高さは何cmですか。
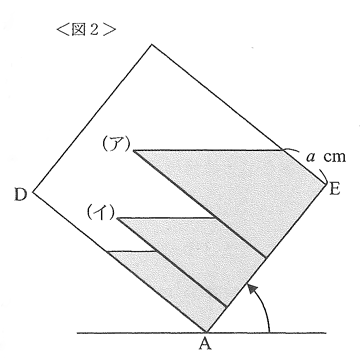
(2)次に、水そうの辺ABを床につけたまま水そうを静かに傾けると、ちょうど<図2>のようになりました。その後、水そうをもとに戻したところ、あ、い、うの部分の水面の高さがちょうど同じになりました。
1 水そうをもとに戻したときの水面の高さは何cmですか。
2 <図2>のaはいくらですか。
3 仕切り(イ)の高さは何cmですか。
【解説と解答】
(1)24×12.5=300cm3 いの部分が高さ5cmなので、3×5×5=75 300-75=225
225÷25=9
(答え)9cm
(2)
1 もとにもどしたときに水の高さがみな同じになったので、300÷(5×10)=6cm
(答え)6cm
2 高さが同じなので、あ、い、うには5:3:2の容積の比で水が入っているので、あに入っている水の領は300÷(5+3+2)×5=150cm3
(9+a)×5÷2×5=150 からa=3
(答え)3cm
3 傾けたときの水面はあ、い、うともに平行になります。したがってAE:AD=9-3:5=6:5ですから
いの台形の部分の面積は300÷10×3=90cm3 90÷5=18cm2ですから、上底(短い辺)を【1】とすると
(【1】+【1】+3÷5×6)×3÷2=18 【2】+3.6=12 【1】=4.2より(イ)は4.2+3.6=7.8
(答え)7.8cm
============================================================
受験で子どもと普通に幸せになる方法、本日の記事は
欲しいのは学習履歴
============================================================
中学受験 算数オンライン塾
9月13日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村