西大和学園の問題です。
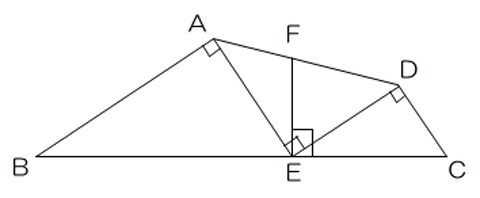
図の四角形ABCDにおいて、三角形AEDは直角二等辺三角形で、角BAE=角EDC=角FEC=90°です。AF:FD=3:4であるとき、三角形AEDと四角形ABCDの面積比を最も簡単な整数比で求めなさい。
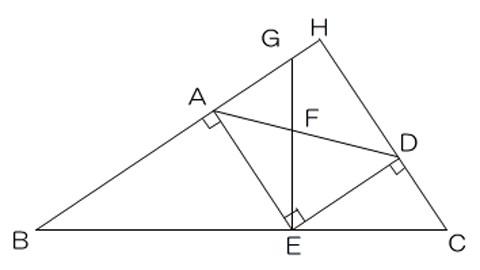
ABとCDを延長して、その交点をHとすると、四角形AEDHは正方形になります。
AF:FD=3:4なので、AG:ED=3:4 AE=ED=【4】とすると、AG=【3】AG:AE=3:4より、AE:AB=3:4 ED:DC=4:3より、DC=【3】 AB=【4】×$$\frac{4}{3}$$=【$$\frac{16}{3}$$】
AB=16 AE=12 ED=12 DC=9より、四角形ABCD=16×12÷2+12×9÷2+12×12÷2=96+54+72=222
三角形AED=72より
222:72=74:24=37:12
(答え)12:37
============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
昼寝を上手にする
============================================================
中学受験 算数オンライン塾
7月5日の問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村
0620