2016年筑波大付属駒場中学の問題です。
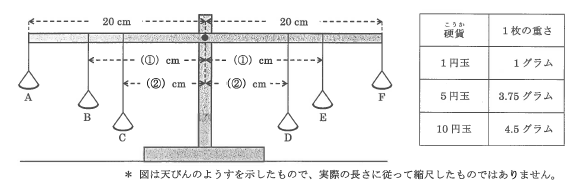
長さ40cmの棒と6つの皿を使って、下図のような天びんを利用した両替機を作った。1円玉(1グラム)、5円玉(3.75g)、10円玉(4.5g)をたくさん用意し、指定された皿にのせた。すると、棒がつりあったときは、左側の3つの皿(皿A〜C)にのっている硬貨の合計金額と、右側の3つの皿(皿D〜F)にのっている硬貨の合計金額が必ず等しくなった。【天びんの作り方】と【天びんの使用方法】を読んで、あとの問いに答えなさい。
【天びんの作り方】
・棒の両はしに糸で皿Aと皿Fをつるした。
・棒の中心から( 1 )cmだけ離れた左右の位置に、皿Bと皿Eをつるした。
・棒の中心から( 2 )cmだけ離れた左右の位置に、皿Cと皿Dをつるした。なお2は1よりも小さい。
・皿がぶつからないように、位置の長さを変えて皿をつるした。
・以上のように6つの皿をつるしたら、棒はつりあった。
【天びんの使用方法】
・( 3 )円玉は、皿Aあるいは皿Fの一方だけにのせることができる。
・( 4 )円玉は、皿Bあるいは皿Eの一方だけにのせることができる。
・( 5 )円玉は、皿Cあるいは皿Dの一方だけにのせることができる。
1 ( 1 )〜( 5 )にあてはまる数を答えなさい。
2 棒がつりあったとき、合計金額だけでなく、左側の3つの皿にのっている硬貨の枚数と右側の3つの皿にのっておりう硬貨の合計枚数が等しくなるときがある。このときに使用した硬貨の総枚数(皿A〜Fにある硬貨の合計枚数)が最も少ないときの各硬貨の枚数を答えなさい。
3 硬貨の総枚数が50枚でつりあった。このとき使用した硬貨の総金額(皿A〜Fにある硬貨の合計金額)が最も多い場合と最も少ない場合について、各硬貨の枚数を答えなさい。必要ならば下の図を利用しなさい。
【解説と解答】
1
左と右の合計金額が同じにならなければなりません。
またどの硬貨も左右どちらかの皿に来るので、1円玉、5円玉、10円玉はABCのどれかとDEFのどれかになり、どちらかにしか硬貨を置くことができません。10円玉を両替すると、5円2枚、1円10枚のように枚数が増えますから、一番外側が10円玉、次が5円玉、一番内側が1円玉である必要があります。
10円玉が1枚Aにあるとすると、4.5×20=90ですから、①×10=90より①=9cm 90÷(3.75×2)=12が②の長さになります。
(答え)1 12 2 9 3 10 4 5 5 1
2 同じ側にあるのが10円玉と1円玉、10円玉と5円玉、5円玉と1円玉である場合があるが、両方とも同じ枚数になることから、同じ側にあるのは10円玉と1円玉である。
10円玉の枚数をA、5円玉の枚数をB、1円玉の枚数をCとすると、
A+C=B
10×A+1×C=5×B
9×A=4×Bなので、Aが4枚、Bが9枚、Cが1枚が最小になります。
(答え)10円 4枚 5円 9枚 1円 5枚
3
10円玉の枚数をA、5円玉の枚数をB、1円玉の枚数をCとすると、総額が一番多いというのは10円玉をなるべく多く使ったときになり、総額が1番小さい場合は10円玉をなるべく使わなかったときになります。
10円玉は5円玉2枚、1円玉10枚と釣り合います。同じ側に5円玉と1円玉にすると、10円と5円玉2枚を釣り合わせて、50÷3=16、から10円玉16枚、5円玉32枚、だと1円玉の使いようがないので、1円玉を10枚、10円玉を1枚にして、残りを5円玉と10円玉に分ければよいので、50-11=39 39÷3=13より10円玉14枚、1円玉10枚、5円玉26枚が金額としては最も多くなります。
(最多)10円玉 14枚、5円玉26枚、1円玉10枚
一番金額を少なくするのは10円玉と5円玉を同じ側にすればよく、1枚ずつ置くと、10円玉で10枚、5円玉で5枚ですから、10円玉4枚と5円玉1枚で、10×4+5×1+4+1=50枚
(最小)10円玉 4枚 5円玉 1枚 1円玉45枚
============================================================
受験で子どもと普通に幸せになる方法、本日の記事は
塾が提供することを全部やれるわけがない
============================================================
中学受験 算数オンライン塾
9月11日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村