2015年桜蔭中学の問題です。
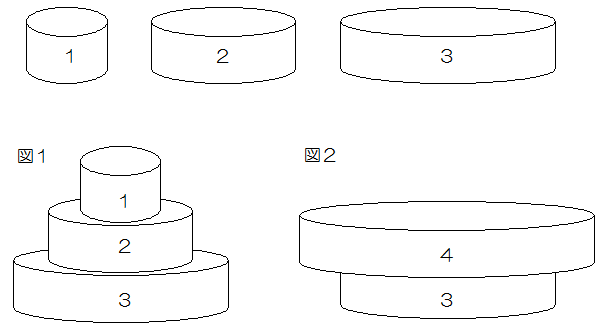
図のように、番号のついたいろいろな大きさの円柱があります。1の円柱の底面の半径は2cmで、番号が1つ増えるごとに底面の半径は、前の番号の円柱の半径の2倍になっています。円柱の高さはすべて3cmです。これらの円柱を何個か積み重ねて新しい立体を作ろうと思います。ただし、円柱の底面の円の中心どうしが重なるように積み重ねます。
図1のように3の上に2、2に上に1を積み重ねた立体を{3、2、1}、図2のように3の上に4を積み重ねた立体を{3、4}のように表すことにします。
このとき、立体{3、2、1}と立体{1、2、3}は同じ立体となります。次の問いに答えなさい。
(1)図1の立体 {3、2、1}の表面積を求めなさい。
(2)立体 {6、3、4、2、5}と立体{6、5、4、3、2}の表面積の差を求めなさい。
(3)1、2、3、4、5の円柱を1つずつ使って立体を作ります。
立体{5、4、3、2、1}と同じ表面積になる{5、4、3、2、1}以外の立体をすべて答えなさい。ただし解答らんの{ア、イ、ウ、エ、オ}において、アはオよりも大きいものとします。
【解説と解答】
(1)3の半径は8cm、2の半径は4cm、1の半径は2cmです。
したがって(8×2×3.14+4×2×3.14+2×2×3.14)×3+8×8×3.14×2=(84+128)×3.14=212×3.14=665.68cm2
(答え)665.68cm2
(2)側面積では差が出ません。
また上から見た底面積と下から見た底面積でも差が出ません。
差は下の図の赤い部分になるので、
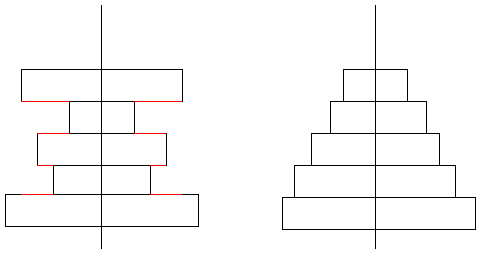
(32×32-4×4+16×16-4×4+16×16-8×8+32×32-8×8)×3.14=(1024-16+256-16+256-64+1024-64)×3.14=2400×3.14=7536cm2
(答え)7536cm2
(3)図のように凸体になればいいことになります。
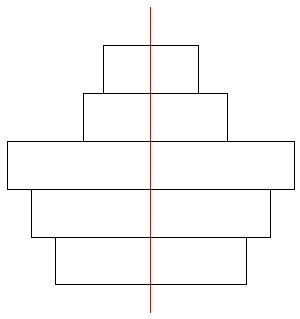
したがって以下の表のように一番大きい5が左から2番目と左から3番目に置いたとき、5までを段々大きく、5からは段々小さくする、という形で並べればいいことになります。
左から4番目は左から2番目と同じになるので、重ならないように注意します。
答えは
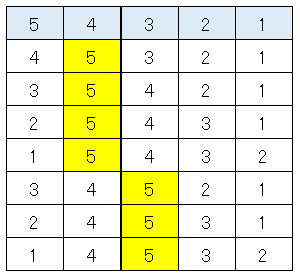
となります。
「映像教材、これでわかる比と図形」(田中貴)
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
なぜ優先順位を決めるのか
=============================================================
中学受験 算数オンライン塾
6月23日の問題
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

