2015年灘中学の問題です。
次の( ア )( イ )にあてはまる数を答えなさい。
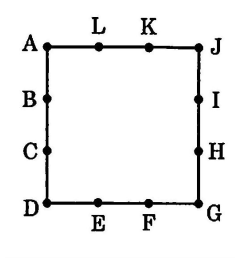
図のように、1辺の長さが6cmの正方形の周上に、AからLまでの点が2cmごとにあります。これらの12個の点から3個の点を選び、それらを頂点とする三角形を作ります。三角形は全部で( ア )個できます。そのうち二等辺三角形は全部で( イ )個です。ただし、合同な三角形であっても、選んだ点が違えば、別の三角形と考えます。
【解説と解答】
( ア )
ぜんぶで12個の点から3個の点を選ぶ組み合わせは
12×11×10÷(3×2×1)=220通りあります。
が、このうち三角形ができないのは同じ辺から3つの点を選んだ場合で、それは各辺4通りずつあります。
したがってできる三角形は220-4×4=204通り
(答え)204通り
( イ )
Bを頂点としたとき、二等辺三角形は三角形BJHとBKEの2通りがあります。
したがってこのような点はBCEFHIKLと8つあるので2×8=16通りです。
一方Aを頂点としたときはALB、AKC、AJD、AIE、AHFと5つあります。Aのような点はA、D、G、Jと4つあるので5×4=20
したがって合計16+20=36通り
(答え)36通り
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
過去問は時間をはからない
==============================================================
中学受験 算数オンライン塾
4月14日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

