2014年白百合学園の問題です。
図は3つの正方形を重ねたもので、点Eは辺ADの真ん中の点です。
アの部分の面積がイの部分の面積の$$\frac{1}{3}$$であるとき、ウの部分の面積は正方形ABCDの何分のいくつですか。
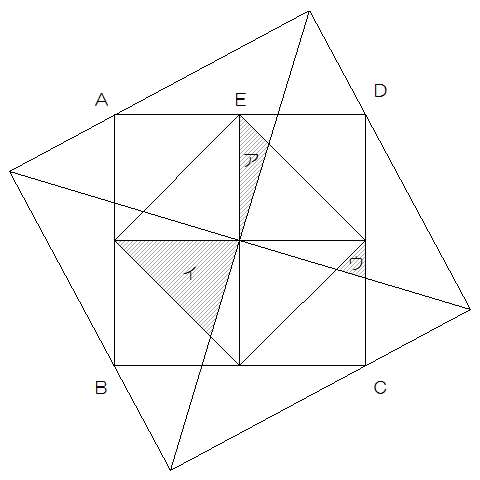
【解説と解答】
イとウの位置を変えると図のようになります。
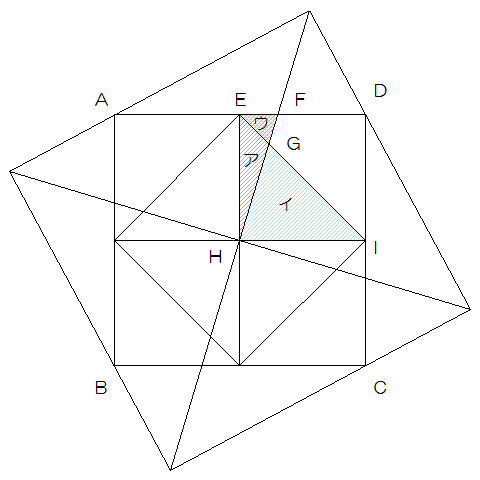
したがってアがイの$$\frac{1}{3}$$であるならばEG:GI=1:3
ウはイの$$\frac{1}{3}$$×$$\frac{1}{3}$$=$$\frac{1}{9}$$です。
アとイの合計は正方形ABCDの$$\frac{1}{8}$$ですから、
イは正方形ABCDの$$\frac{1}{8}$$×$$\frac{3}{4}$$
ウは正方形ABCDの$$\frac{1}{8}$$×$$\frac{3}{4}$$×$$\frac{1}{9}$$=$$\frac{1}{96}$$になります。
(答え)$$\frac{1}{96}$$
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
前倒しの余波
==============================================================
中学受験 算数オンライン塾
8月19日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

