2017年筑波大駒場中学の問題です。
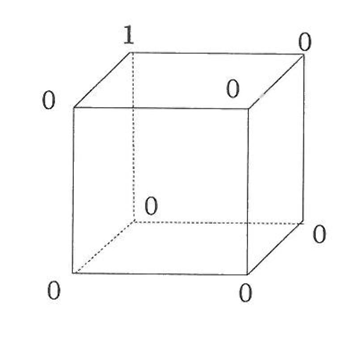
立方体の各頂点に0または1をおきます。立方体のそれぞれの面について、頂点においた4つの数の和を『面の値』ということにし、6個の『面の値』の合計を考えます。
例えば、1個の1と7個の0を右図のように頂点においたとき、『面の値』が1である面が3個、0である面が3個なので、6個の『面の値』の合計は3です。
次の問いに答えなさい。
(1)6個の『面の値』の合計が6になりました。
(ア)1をおいた頂点は何個ありますか。
(イ)『面の値』が奇数である面は何個ありますか。考えられる個数をすべて答えなさい。
(2)6個の『面の値』の合計が12になりました。6個の頂点への0と1のおき方は何通りありますか。
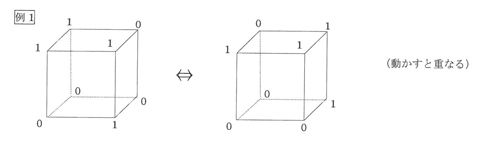
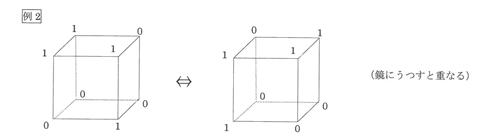
ただし、立方体を動かすと重なるものや、鏡にうつすと重なるものは同じおき方とします。例えば、下の例1、例2はそれぞれ同じおき方です。
【解説と解答】
(1)
(ア)頂点には0か1しかありません。1つの頂点に1を置くと、その1は3面で数えられますから、和は3になります。したがって値が6であるならば6÷3=2個です。
(答え)2個
(イ)1つの面に頂点は4つありますから、2個1を置けば、0、1、2のどれかになります。したがって奇数は1だけです。
上図から1は2個、4個、6個になります。
(答え)2個、4個、6個
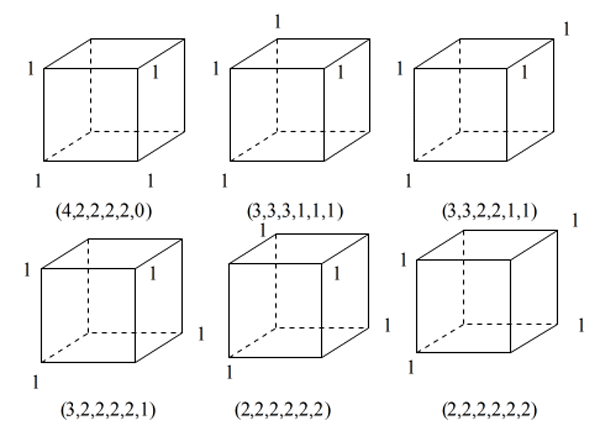
(2)和が12ですから1は4個置かれたことになります。したがって0が4個、1が4個です。
A)1つの正方形の4つの頂点に置かれる場合。
B)1つの正方形の3つの頂点ともう1個置かれる場合。
C)1つの正方形の2つの頂点ともう2個置かれる場合。
の3通りに分けることができます。
Aは1通り。
Bは3通り。
Cは2通り。あるので合計6通りになります。
(答え)6通り
受験で子どもと普通に幸せになる方法、本日の記事は
塾に行かせる前に
6年生の教室から
出題傾向が変わらないのは
中学受験 算数オンライン塾
5月23日の問題