2014年立教池袋中学の問題です。
図のような3種類の正三角形のカードがたくさんあります。これらを重ならないようにすきまなく並べて、1辺が7cmの正三角形を作ります。
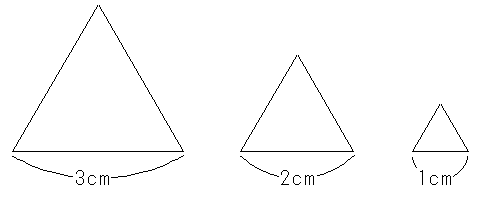
ただし、3種類のカードはそれぞれ少なくとも1枚は使います。
次の問いに答えなさい。
(1)3種類のカードの合計枚数が最も多いときは、何枚ですか。
(2)3種類のカードの合計枚数が最も少ないときは、何枚ですか。
(1)1辺が3cmの正三角形は1辺が1cmの正三角形1+3+5=9個でできています。
1辺が2cmの正三角形は1辺が1cmの正三角形1+3=4個でできています。
1辺が7cmの正三角形は1辺が1cmの正三角形1+3+5+9+11+13=(1+13)×7÷2=49個でできています。
したがって1辺が3cmの正三角形1個と1辺が2cmの正三角形1個、あとはすべて1辺が1cmの正三角形にすると
1辺が1cmの正三角形は49-9-4=36個ですから、合計1+1+36=38個です。
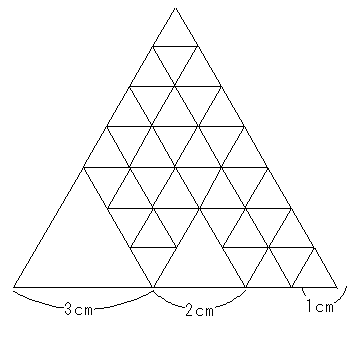
(答え)38個
(2)
9と4と1をなるべく少なく組み合わせて49を作ることを考えます。
9を3枚使うと、残りは49-27=22 22で4を5枚使うことはできません。
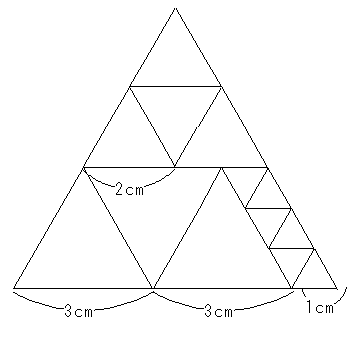
したがって1を6枚使うことになるので、3+4+6=13枚です。
ただ1辺が7cmなので、3cmを2枚にしてなるべく2cmの正三角形を多く使うことを考え、1cmの正三角形をなるべく使わないようにします。
すると9×2+4×7+1×3=49が成り立ちます。
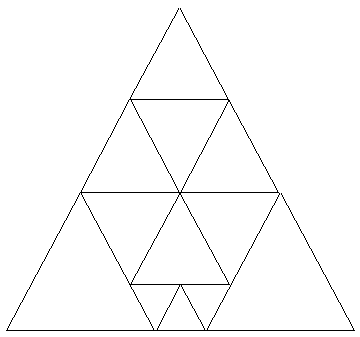
したがって12枚が最小になります。
(答え)12枚
===========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
入試応援に行かない塾
==============================================================
今日の慶應義塾進学情報
解答用紙は基本的に1枚
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村
