2014年 白百合学園の問題です。
図のように、辺ADとBCを平行とした台形を底面とする四角柱の容器があります。辺BC上に、辺AIと辺BCが垂直となるように点Iをとり、辺BIの長さは1cm、辺CIの長さは3cm、辺ADの長さは5cm、辺BEの長さは35cmとします。

いま、この容器の底面に垂直に、2つの仕切り板を入れることにしました。1枚はAとIを通るように、もう1枚はDとIを通るように入れることで、3つの容器に分けています。
ここで、辺ABを含む容器をア、辺ADを含む容器をイ、辺CDを含む容器をウとし、3つの容器に同じ量だけ水を入れました。仕切り板の厚さは考えないものとします。
(1)容器ア、イ、ウに同じ量だけ水が入っているとき、容器イだけの水面の高さを測ったら6cmでした。この状態から容器イとウの間の仕切り板だけを外したときの容器イ・ウの水面の高さは何cmになりますか。
(2)(1)のように、容器イとウの間の仕切り板が外された状態から、さらに容器アとイの間の仕切り板も外したとき、この四角柱の水面の高さは何cmになりますか。
(3)(2)のように、仕切り板がすべて外された状態から、さらにこの容器の中に、半径2cm、高さ20cmの円柱を垂直に下まで入れたとき、水面の高さは何cmになりますか。ただし、AIの長さは8cm、円周率は$$\frac{22}{7}$$とします。
【解説と解答】
(1)底面を見るとこのようになっています。
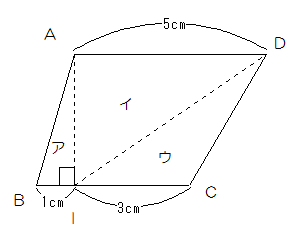
このとき、ア、イ、ウはすべてAIを高さとしているので、面積比はア:イ:ウ=1:5:3です。底面積をア、イ、ウそれぞれ【1】、【5】、【3】とするとイの高さが6cmならば、容積は【30】になるので、アも【30】、ウも【30】です。で、イとウの容積は【60】になり、しきりをはずすと面積は8になるのだから、
【60】÷8=7.5cmになります。
(答え)7.5cm
(2)今度は容積が【90】になり、底面積が【9】ですから、【90】÷【9】=10cmです。
(答え)10cm
(3)AIの長さが8cmになるので、台形ABCDの面積は36cm2になります。
水の容積は36×10=360cm3
一方円柱の底面積は2×2×$$\frac{22}{7}$$=$$\frac{88}{7}$$
36-$$\frac{88}{7}$$=$$\frac{164}{7}$$
360÷$$\frac{164}{7}$$=$$\frac{2520}{164}$$=$$\frac{630}{41}$$=15$$\frac{15}{41}$$<20cmなので、円柱はすべて水没しないことで間違いありません。
(答え)15$$\frac{15}{41}$$cm
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
準備をやりきる
==============================================================
今日の慶應義塾進学情報
選挙の問題
==============================================================

==============================================================
==============================================================

==============================================================
![]()

