2015年東邦大東邦の問題です。
次の問いに答えなさい。ただし、円周率は3.14とします。
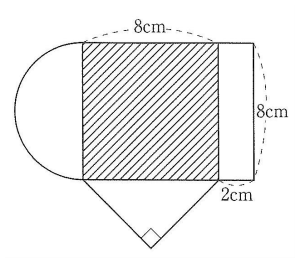
(1)次の図のように1辺の長さが8cmの正方形に、半円と直角二等辺三角形と長方形をつけた図形を紙で作りました。この半円と直角二等辺三角形と長方形を、正方形の辺を折り目として内側に折り返したとき、斜線部分で見えている部分の面積を求めなさい。
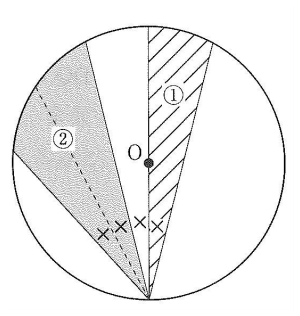
(2)次の図の部分①と部分②の面積をそれぞれ求めなさい。
ただし、点0は円の中心で、円の半径は6cm、×印のついた角の大きさは15°です。
【解説と解答】
(1)
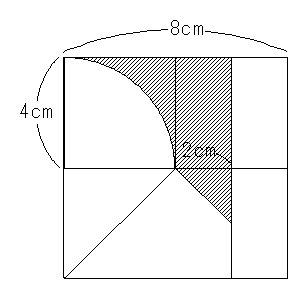
図のようになるので、残るのは
4×4-4×4×3.14÷4+4×2+2×2÷2=13.44cm2
(答え)13.44cm2
(2)
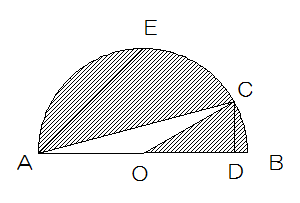
角CAOは15°です。
したがって角CODは30°になるので、CからABにおろした垂線とABの交点をDとしたとき、直角三角形OCDは正三角形の半分ですから、OC=6㎝ CD=3cm
①の面積は三角形AOCとおおぎ形OCBの和になりますから6×3÷2+6×6×3.14÷12=9+9.42=18.42cm2です。
また②の面積は4分の1円EOBと直角三角形EOAの和から①の面積を引けばいいので
6×6×3.14÷4+6×6÷2-18.42=28.26+18-18.42=27.84
(答え)27.84cm2
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
安全校選び
==============================================================
今日の慶應義塾進学情報
中等部の算数の解答用紙
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

