2017年駒場東邦の問題です。
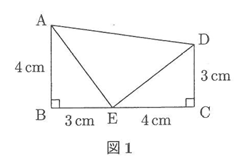
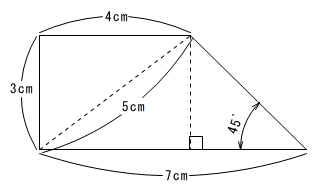
(1)図1のように台形ABCDと辺BC上に点Eがあります。次のものを求めなさい。
1)三角形AEDの面積
2)三角形AEDの辺AEの長さ
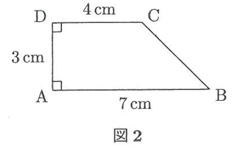
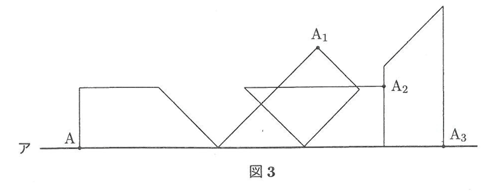
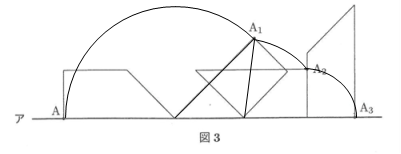
(2)図2のような台形ABCDがあります。この台形を図3のように直線ア上をすべらないように転がし,点Aが再び直線ア上に来たら止まるものとします。このとき,頂点AはA→Al→A2→A3と動きます。点Aが動いてできる線イを解答用紙の図にコンパスを用いてかきなさい。また,次のものを求めなさい。ただし,円周率は3.14とします。
1)線イの長さ
2)線イと直線アによって囲まれる部分の面積
【解説と解答】
(1)
1)
台形ABCDから2つの直角三角形を引けば良いので、(4+3)×(4+3)÷2-4×3÷2×2=24.5-12=12.5
(答え)12.5cm2
2)
三角形AEDを2倍すれば正方形になるので、12.5×2=25cm2 これは5×5ですから1辺は5cm
(答え)5cm
(2)
1)
となるので、A1までは135度 A1からA2までは180-45-90=45度 A2からA3までは90度になるので、
7×2×3.14×$$\frac{3}{8}$$+5×2×3.14×$$\frac{1}{8}$$+3×2×3.14×$$\frac{1}{4}$$
=($$\frac{21}{4}$$+$$\frac{5}{4}$$+$$\frac{6}{4}$$)×3.14=8×3.14=25.12
(答え)25.12cm
2)
7×7×3.14×$$\frac{3}{8}$$+5×5×3.14×$$\frac{1}{8}$$+3×3×3.14×$$\frac{1}{4}$$+(7+4)×3÷2
=($$\frac{147}{8}$$+$$\frac{25}{8}$$+$$\frac{18}{8}$$)×3.14+15=23.75×3.14+16.5=91.075cm2
(答え)91.075cm2
受験で子どもと普通に幸せになる方法、本日の記事は
今のままで良いか?
6年生の教室から
夏の勉強を考える
中学受験 算数オンライン塾
5月31日の問題